Question

Đã trả lời bởi chuyên gia

Answer 1

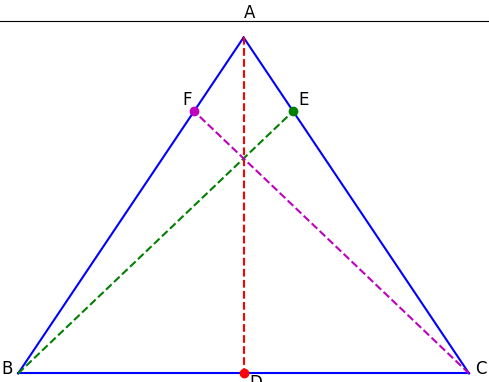
Hỏi đáp VietJack

- Xét tứ giác BCEF:
+ BE là đường cao của tam giác ABC, nên BE $⊥$ AC. Do đó, $\hat{B E C} = 90^{\circ}$ .
+ CF là đường cao của tam giác ABC, nên CF $⊥$ AB. Do đó, $\hat{B F C} = 90^{\circ}$ .
Vì: Hai đỉnh E và F cùng nhìn cạnh BC dưới một góc 90 $°$ .
=> Tứ giác BCEF có hai đỉnh kề E, F cùng nhìn cạnh BC dưới một góc vuông.
Do đó, BCEF là tứ giác nội tiếp đường tròn đường kính BC.
- Xét tứ giác CAFD:
+ AD là đường cao của tam giác ABC, nên AD $⊥$ BC. Do đó, $\hat{A D C} = 90^{\circ}$ .
+ CF là đường cao của tam giác ABC, nên CF $⊥$ AB. Do đó, $\hat{C F A} = 90^{\circ}$ .
Vì: Hai đỉnh D và F cùng nhìn cạnh AC dưới một góc 90 $°$ .
=> Tứ giác CAFD có hai đỉnh kề D, F cùng nhìn cạnh AC dưới một góc vuông.
Do đó, CAFD là tứ giác nội tiếp đường tròn đường kính AC.|
- Xét tứ giác ABDE:
+ AD là đường cao của tam giác ABC, nên AD $⊥$ BC. Do đó, $\hat{A D B} = 90^{\circ} .$
+ BE là đường cao của tam giác ABC, nên BE $⊥$ AC. Do đó, $\hat{A E B} = 90^{\circ}$ .
Vì: Hai đỉnh D và E cùng nhìn cạnh AB dưới một góc 90 $°$ .
=> Tứ giác ABDE có hai đỉnh kề D, E cùng nhìn cạnh AB dưới một góc vuông.
Do đó, ABDE là tứ giác nội tiếp đường tròn đường kính AB.

...Xem thêm

Answer 2

Hỏi đáp VietJack

- Xét tứ giác BCEF:
+ BE là đường cao của tam giác ABC, nên BE $⊥$ AC. Do đó, $\hat{B E C} = 90^{\circ}$ .
+ CF là đường cao của tam giác ABC, nên CF $⊥$ AB. Do đó, $\hat{B F C} = 90^{\circ}$ .
Vì: Hai đỉnh E và F cùng nhìn cạnh BC dưới một góc 90 $°$ .
=> Tứ giác BCEF có hai đỉnh kề E, F cùng nhìn cạnh BC dưới một góc vuông.
Do đó, BCEF là tứ giác nội tiếp đường tròn đường kính BC.
- Xét tứ giác CAFD:
+ AD là đường cao của tam giác ABC, nên AD $⊥$ BC. Do đó, $\hat{A D C} = 90^{\circ}$ .
+ CF là đường cao của tam giác ABC, nên CF $⊥$ AB. Do đó, $\hat{C F A} = 90^{\circ}$ .
Vì: Hai đỉnh D và F cùng nhìn cạnh AC dưới một góc 90 $°$ .
=> Tứ giác CAFD có hai đỉnh kề D, F cùng nhìn cạnh AC dưới một góc vuông.
Do đó, CAFD là tứ giác nội tiếp đường tròn đường kính AC.|
- Xét tứ giác ABDE:
+ AD là đường cao của tam giác ABC, nên AD $⊥$ BC. Do đó, $\hat{A D B} = 90^{\circ} .$
+ BE là đường cao của tam giác ABC, nên BE $⊥$ AC. Do đó, $\hat{A E B} = 90^{\circ}$ .
Vì: Hai đỉnh D và E cùng nhìn cạnh AB dưới một góc 90 $°$ .
=> Tứ giác ABDE có hai đỉnh kề D, E cùng nhìn cạnh AB dưới một góc vuông.
Do đó, ABDE là tứ giác nội tiếp đường tròn đường kính AB.

Answer 3

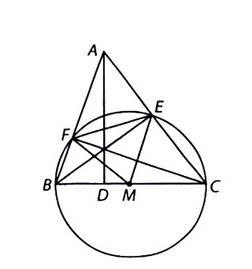
Lấy M là trung điểm của BC. Do BCE, BCF là các tam giác vuông có chung cạnh huyền BC nên ME = MB = MC = MF. Do đó đường tròn (M, MB) ngoại tiếp tứ giác BCEF.

Tương tự, CAFD và ABDE cũng là các tứ giác nội tiếp.

2 câu trả lời 360

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 9