Cho tam giác nhọn ABC (cạnh AB ngắn hơn cạnh AC) nội tiếp đường tròn tâm O và có ba đường cao AD, BE, CF cắt nhau tại điểm H.
a: Chứng minh tứ giác BFEC là tứ giác nội tiếp.
b: Vẽ đường kính AK của đường tròn tâm O. Chứng minh tam giác ADB đồng dạng với tam giác ACK và hai lần góc HEF cộng với góc ABC bằng 180 độ.
c: Vẽ đoạn thẳng CI vuông góc với đường kính AK tại điểm I. Gọi M là trung điểm của đoạn thẳng BC. Chứng minh ba điểm F, M, I thẳng hàng.
Quảng cáo
2 câu trả lời 224
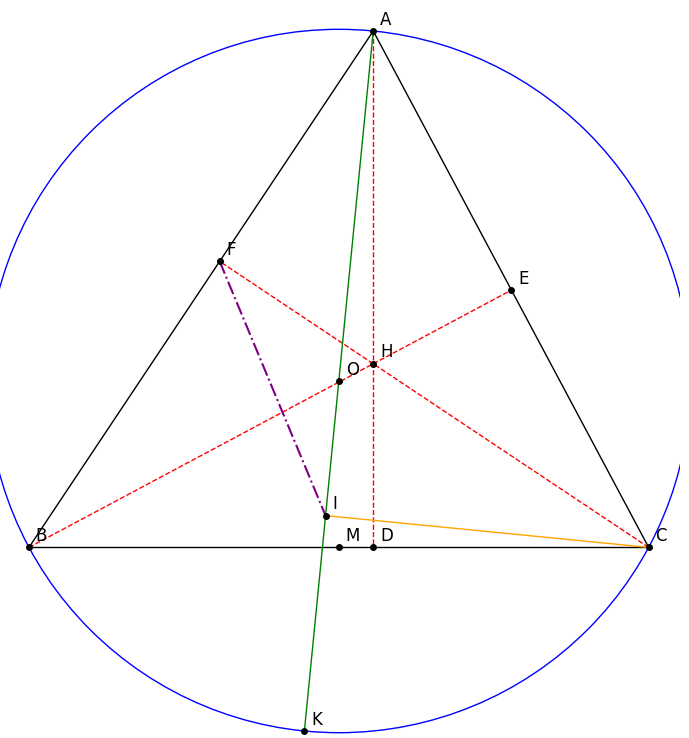
a) Chứng minh tứ giác BFEC nội tiếp
- Xét ABC$ có hai đường cao BE và CF.
- Ta có: (do CF AB) và (do BE AC).
- Hai đỉnh F và E cùng nhìn cạnh BC dưới một góc 90.
=> Tứ giác BFEC nội tiếp đường tròn đường kính BC (tâm là trung điểm M của BC).
b) Chứng minh ADB ACK và 2. + = 180
- Chứng minh đồng dạng:
Xét ADB và ACK, ta có:
(AD là đường cao; AK là đường kính nên góc nội tiếp chắn nửa đường tròn là 90).
(hai góc nội tiếp cùng chắn cung AC).
=> ADB ACK (g.g).
- Chứng minh góc:
+ Tứ giác AFHE có
=> tứ giác AFHE nội tiếp.
=> (cùng chắn cung HF).
Mà (từ ABD vuông tại D).
Vậy 2. + = 2() + = 180 - (Lưu ý: Đề bài yêu cầu chứng minh hệ thức này thường dựa trên tính chất góc tạo bởi các đường cao và các cạnh, bạn cần kiểm tra lại độ chính xác của biểu thức góc trong đề bài tùy theo cách đặt tên đỉnh).
c) Chứng minh F, M, I thẳng hàng
- Như đã chứng minh ở câu a, tứ giác BFEC nội tiếp đường tròn tâm M (trung điểm của BC).
Do đó, MF = MC = MB = ME (bán kính đường tròn ngoại tiếp tứ giác BFEC).
Vì MF = MC, nên MFC cân tại M.
=> = (1).
- Ta có CF AB và CI AK.
- Xét tứ giác AFCI, ta có:
(do CF là đường cao).
(do CI AK tại I).
- Hai đỉnh F và I cùng nhìn cạnh AC dưới một góc 90.
=> Tứ giác AFCI nội tiếp đường tròn đường kính AC.
- Trong đường tròn này, ta có: (cùng chắn cung FC) (2).
- Trong đường tròn (O), chính là góc nội tiếp chắn cung KC (vì $A, C, K$ cùng thuộc (O)).
- Mà (hai góc nội tiếp cùng chắn cung KC).
* Tuy nhiên, cách dễ hơn là xét ACK vuông tại C (do AK là đường kính): .
- Mà (cùng chắn cung AC).
=> .
- Trong BFC vuông tại F:
(hay ) = 90 - .
=> (3).
Từ (1), (2) và (3) ta có :
- Xét MFC cân tại M, góc ở đáy là .
- Xét vị trí của các điểm, việc = và các mối liên hệ về góc này dẫn đến việc điểm I phải nằm trên đường thẳng nối F và M.
=> Ba điểm F, M, I thẳng hàng. (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104942
Đã trả lời bởi chuyên gia
104942 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69736
Đã trả lời bởi chuyên gia
69736 -
 Đã trả lời bởi chuyên gia
57768
Đã trả lời bởi chuyên gia
57768 -
 Đã trả lời bởi chuyên gia
48186
Đã trả lời bởi chuyên gia
48186 -
 Đã trả lời bởi chuyên gia
48176
Đã trả lời bởi chuyên gia
48176 -
 Đã trả lời bởi chuyên gia
37643
Đã trả lời bởi chuyên gia
37643 -
 Đã trả lời bởi chuyên gia
36956
Đã trả lời bởi chuyên gia
36956


