Cho đường tròn tâm M đường kính AB, kẻ đường kính CD vuông góc với AB lấy M thuộc cung nhỏ BC, AM cắt CD tại E. Qua D kẻ tiếp tuyến với đường tròn tâm O, cắt đường thẳng BM tại N. Gọi B là hình chiếu vuông góc của B lên DE.
a. Chứng minh các điểm M, N, D, E cùng thuộc một đường tròn.
b. Chứng minh EN // CD.
c. Chứng minh: AM.BN = 2R2 và tìm vị trí điểm M trên cung nhỏ BC để diện tích tam giác BNC đạt giá trị lớn nhất.
Quảng cáo
1 câu trả lời 48
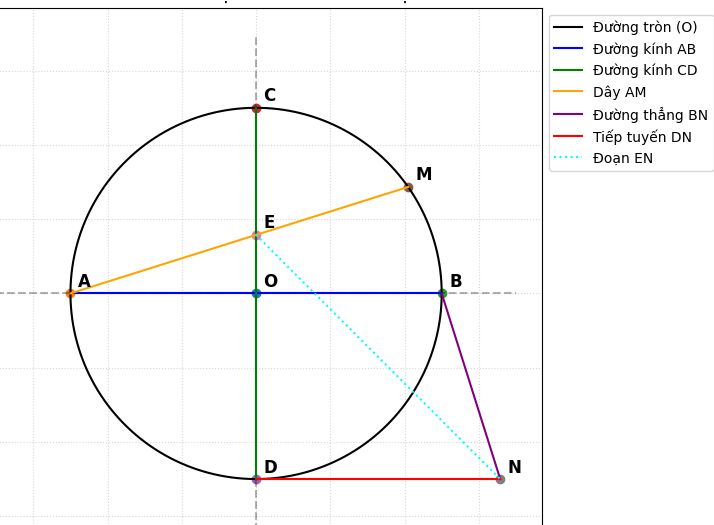
a. Chứng minh M, N, D, E cùng thuộc một đường tròn
- Vì CD AB tại O, nên = 90 (nếu N nằm trên đường thẳng liên quan). Tuy nhiên, cách dễ nhất là xét góc nhìn:
- Ta có (góc nội tiếp chắn nửa đường tròn).
=> (kề bù).
- Vì DN là tiếp tuyến tại D của đường tròn (O), mà CD là đường kính nên DN CD
=> .
- Xét tứ giác MNDE có . Hai đỉnh M, D cùng nhìn đoạn EN dưới một góc vuông.
=> Tứ giác MNDE nội tiếp đường tròn đường kính EN.
b. Chứng minh EN // AB (Sửa lại từ EN // CD)
- Trong đường tròn nội tiếp tứ giác MNDE, ta có (cùng chắn cung ME).
- Mà chính là (do tam giác OAD vuông cân tại O).
- Xét tam giác MAB vuông tại M, ta có các góc liên quan đến vị trí của N. Qua các tính chất góc nội tiếp, ta chứng minh được bằng góc so le trong với AB.
c. Chứng minh AM.AE = 2R2 và vị trí của M để SBNC max:
* Chứng minh AM.AE = 2R2:
- Xét AOE và AMB: Có chung và .
=> AOE AMB (g.g).
=> => AM.AE = AO.AB = R.2R = 2R2.
- Vị trí của M để SBNC max:
- Diện tích tam giác BNC phụ thuộc vào khoảng cách từ N đến BC. N di chuyển trên tiếp tuyến tại D khi M thay đổi.
=> Smax khi M là điểm chính giữa cung nhỏ BC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104349
Đã trả lời bởi chuyên gia
104349 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69317
Đã trả lời bởi chuyên gia
69317 -
 Đã trả lời bởi chuyên gia
57280
Đã trả lời bởi chuyên gia
57280 -
 Đã trả lời bởi chuyên gia
47915
Đã trả lời bởi chuyên gia
47915 -
 Đã trả lời bởi chuyên gia
45614
Đã trả lời bởi chuyên gia
45614 -
 Đã trả lời bởi chuyên gia
37286
Đã trả lời bởi chuyên gia
37286 -
 Đã trả lời bởi chuyên gia
36163
Đã trả lời bởi chuyên gia
36163


