Từ 1 điểm A nằm ngoài đường tròn (O,R) kẻ hai tiếp tuyến AB,AC với (O,R) (B và C là hai tiếp điểm ). Gọi H là giao điểm của OA và BC và I là trung điểm của OA
a. Chứng minh 4 điểm A, B, O, C cùng thuộc 1 đường tròn và AB2 = AH.AO
b. Vẽ đường kính BD của (O). Đường thằng qua O và vuông góc với AD cắt tia BC tại E. Chứng minh DE là tiếp tuyến của (O)
c. Cho biết OA = 10cm và R = 5cm. Tính phần diện tích mặt phẳng giới hạn bởi AB, AC và cung nhỏ BC của (O). (Kết quả làm tròn đến hàng phần mười)
Quảng cáo
2 câu trả lời 73
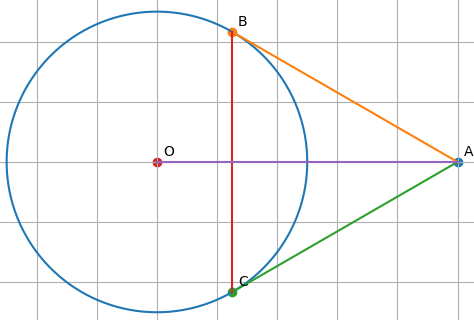
a) Chứng minh A, B, O, C cùng thuộc một đường tròn và AB2=AH.AO
* Chứng minh tứ giác ABOC nội tiếp
- Vì AB, AC là tiếp tuyến nên: OB ⊥ AB, OC ⊥ AC
=> = = 90∘
=> Hai góc đối của tứ giác ABOC bù nhau
⇒ A, B, O, C cùng thuộc một đường tròn
* Chứng minh AB2 = AH.AO
BC là dây tiếp điểm, nên: BC ⊥ AO
⇒ H là chân đường cao từ B xuống AO
- Xét tam giác vuông ABO, có BH ⊥ AO
- Áp dụng hệ thức lượng trong tam giác vuông: AB2 = AH.AO (đpcm)
b) Chứng minh DE là tiếp tuyến của (O)
- Ta có:
BD là đường kính ⇒ O là trung điểm của BD
=> Kẻ OE ⊥ AD: Vì BC là đường cực của A nên: E nằm trên BC
- Ta có:
OE ⊥ DE Mà OE là bán kính ⇒ DE là tiếp tuyến của (O)
c) Tính diện tích hình giới hạn bởi AB, AC và cung nhỏ BC
- Độ dài tiếp tuyến:
- Góc ở tâm: => = 60∘ ⇒ = 120∘
=> Diện tích cần tìm: S = S△ABC − Squạt BOC
- Diện tích tam giác ABC là: S△ABC = .BC.AH với:
BC = 2.R.sin60∘ = , AH = = = 7.5
⇒ S△ABC = 7.5 ≈ 32.5
- Diện tích quạt tròn: Squạt =
Vậy: S ≈ 6.3 cm2
➡️ Bước 1: Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn và AB2=AH⋅AOcap A cap B squared equals cap A cap H center dot cap A cap O
𝐴𝐵2=𝐴𝐻⋅𝐴𝑂
Vì AB,ACcap A cap B comma cap A cap C
𝐴𝐵,𝐴𝐶
là hai tiếp tuyến của (O,R)open paren cap O comma cap R close paren
(𝑂,𝑅)
nên AB⟂OBcap A cap B ⟂ cap O cap B
𝐴𝐵⟂𝑂𝐵
và AC⟂OCcap A cap C ⟂ cap O cap C
𝐴𝐶⟂𝑂𝐶
. Suy ra ∠ABO=90∘angle cap A cap B cap O equals 90 raised to the composed with power
∠𝐴𝐵𝑂=90∘
và ∠ACO=90∘angle cap A cap C cap O equals 90 raised to the composed with power
∠𝐴𝐶𝑂=90∘
.
Xét tứ giác ABOCcap A cap B cap O cap C
𝐴𝐵𝑂𝐶
có ∠ABO+∠ACO=90∘+90∘=180∘angle cap A cap B cap O plus angle cap A cap C cap O equals 90 raised to the composed with power plus 90 raised to the composed with power equals 180 raised to the composed with power
∠𝐴𝐵𝑂+∠𝐴𝐶𝑂=90∘+90∘=180∘
, do đó tứ giác ABOCcap A cap B cap O cap C
𝐴𝐵𝑂𝐶
nội tiếp đường tròn đường kính OAcap O cap A
𝑂𝐴
. Vậy A,B,O,Ccap A comma cap B comma cap O comma cap C
𝐴,𝐵,𝑂,𝐶
cùng thuộc một đường tròn.
Theo tính chất hai tiếp tuyến cắt nhau, ta có AB=ACcap A cap B equals cap A cap C
𝐴𝐵=𝐴𝐶
và AOcap A cap O
𝐴𝑂
là tia phân giác của ∠BACangle cap B cap A cap C
∠𝐵𝐴𝐶
. Suy ra AO⟂BCcap A cap O ⟂ cap B cap C
𝐴𝑂⟂𝐵𝐶
tại Hcap H
𝐻
.
Xét △ABOtriangle cap A cap B cap O
△𝐴𝐵𝑂
vuông tại Bcap B
𝐵
có đường cao BHcap B cap H
𝐵𝐻
, áp dụng hệ thức lượng trong tam giác vuông ta có: AB2=AH⋅AOcap A cap B squared equals cap A cap H center dot cap A cap O
𝐴𝐵2=𝐴𝐻⋅𝐴𝑂
.
➡️ Bước 2: Chứng minh DE là tiếp tuyến của (O)
Xét △BCDtriangle cap B cap C cap D
△𝐵𝐶𝐷
có Ocap O
𝑂
là trung điểm của BDcap B cap D
𝐵𝐷
và Hcap H
𝐻
là trung điểm của BCcap B cap C
𝐵𝐶
(do OA⟂BCcap O cap A ⟂ cap B cap C
𝑂𝐴⟂𝐵𝐶
tại Hcap H
𝐻
). Vậy OHcap O cap H
𝑂𝐻
là đường trung bình của △BCDtriangle cap B cap C cap D
△𝐵𝐶𝐷
, suy ra OH∥CDcap O cap H is parallel to cap C cap D
𝑂𝐻∥𝐶𝐷
hay OA∥CDcap O cap A is parallel to cap C cap D
𝑂𝐴∥𝐶𝐷
.
Gọi Kcap K
𝐾
là giao điểm của OEcap O cap E
𝑂𝐸
và ADcap A cap D
𝐴𝐷
. Theo giả thiết OE⟂ADcap O cap E ⟂ cap A cap D
𝑂𝐸⟂𝐴𝐷
tại Kcap K
𝐾
.
Vì OA∥CDcap O cap A is parallel to cap C cap D
𝑂𝐴∥𝐶𝐷
, theo định lý Ta-lét và tính chất tam giác đồng dạng, ta có thể chứng minh được △EOB=△EODtriangle cap E cap O cap B equals triangle cap E cap O cap D
△𝐸𝑂𝐵=△𝐸𝑂𝐷
(hoặc sử dụng tính chất đối xứng qua đường trung trực). Cụ thể, Ocap O
𝑂
nằm trên đường trung trực của BDcap B cap D
𝐵𝐷
, và từ các góc so le trong do OA∥CDcap O cap A is parallel to cap C cap D
𝑂𝐴∥𝐶𝐷
, ta chứng minh được ∠EOB=∠EODangle cap E cap O cap B equals angle cap E cap O cap D
∠𝐸𝑂𝐵=∠𝐸𝑂𝐷
.
Xét △EOBtriangle cap E cap O cap B
△𝐸𝑂𝐵
và △EODtriangle cap E cap O cap D
△𝐸𝑂𝐷
có: OB=OD=Rcap O cap B equals cap O cap D equals cap R
𝑂𝐵=𝑂𝐷=𝑅
, OEcap O cap E
𝑂𝐸
chung, ∠EOB=∠EODangle cap E cap O cap B equals angle cap E cap O cap D
∠𝐸𝑂𝐵=∠𝐸𝑂𝐷
. Do đó △EOB=△EOD (c.g.c)triangle cap E cap O cap B equals triangle cap E cap O cap D (c.g.c)
△𝐸𝑂𝐵=△𝐸𝑂𝐷 (c.g.c)
.
Suy ra ∠EDO=∠EBO=90∘angle cap E cap D cap O equals angle cap E cap B cap O equals 90 raised to the composed with power
∠𝐸𝐷𝑂=∠𝐸𝐵𝑂=90∘
. Vậy ED⟂ODcap E cap D ⟂ cap O cap D
𝐸𝐷⟂𝑂𝐷
tại Dcap D
𝐷
, nên DEcap D cap E
𝐷𝐸
là tiếp tuyến của (O)open paren cap O close paren
(𝑂)
.
➡️ Bước 3: Tính diện tích phần mặt phẳng giới hạn bởi AB, AC và cung nhỏ BC
Tính các độ dài: AB=OA2−OB2=102−52=75=53 cmcap A cap B equals the square root of cap O cap A squared minus cap O cap B squared end-root equals the square root of 10 squared minus 5 squared end-root equals the square root of 75 end-root equals 5 the square root of 3 end-root cm
𝐴𝐵=𝑂𝐴2−𝑂𝐵2√=102−52√=75√=53√ cm
.
Tính góc ở tâm: Trong △ABOtriangle cap A cap B cap O
△𝐴𝐵𝑂
vuông tại Bcap B
𝐵
, cos∠AOB=OBOA=510=12⟹∠AOB=60∘cosine angle cap A cap O cap B equals the fraction with numerator cap O cap B and denominator cap O cap A end-fraction equals five-tenths equals one-half ⟹ angle cap A cap O cap B equals 60 raised to the composed with power
cos∠𝐴𝑂𝐵=𝑂𝐵𝑂𝐴=510=12⟹∠𝐴𝑂𝐵=60∘
. Do đó ∠BOC=2⋅∠AOB=120∘angle cap B cap O cap C equals 2 center dot angle cap A cap O cap B equals 120 raised to the composed with power
∠𝐵𝑂𝐶=2⋅∠𝐴𝑂𝐵=120∘
.
Diện tích tứ giác ABOCcap A cap B cap O cap C
𝐴𝐵𝑂𝐶
: SABOC=2⋅SABO=2⋅12⋅AB⋅OB=53⋅5=253 cm2cap S sub cap A cap B cap O cap C end-sub equals 2 center dot cap S sub cap A cap B cap O end-sub equals 2 center dot one-half center dot cap A cap B center dot cap O cap B equals 5 the square root of 3 end-root center dot 5 equals 25 the square root of 3 end-root cm squared
𝑆𝐴𝐵𝑂𝐶=2⋅𝑆𝐴𝐵𝑂=2⋅12⋅𝐴𝐵⋅𝑂𝐵=53√⋅5=253√ cm2
.
Diện tích hình quạt tròn OBCcap O cap B cap C
𝑂𝐵𝐶
(cung nhỏ): Squat=π⋅R2⋅120360=π⋅523=25π3 cm2cap S sub q u a t end-sub equals the fraction with numerator pi center dot cap R squared center dot 120 and denominator 360 end-fraction equals the fraction with numerator pi center dot 5 squared and denominator 3 end-fraction equals the fraction with numerator 25 pi and denominator 3 end-fraction cm squared
𝑆𝑞𝑢𝑎𝑡=𝜋⋅𝑅2⋅120360=𝜋⋅523=25𝜋3 cm2
.
Diện tích cần tìm S=SABOC−Squatcap S equals cap S sub cap A cap B cap O cap C end-sub minus cap S sub q u a t end-sub
𝑆=𝑆𝐴𝐵𝑂𝐶−𝑆𝑞𝑢𝑎𝑡
:
S=253−25π3≈43,301−26,180=17,121 cm2cap S equals 25 the square root of 3 end-root minus the fraction with numerator 25 pi and denominator 3 end-fraction is approximately equal to 43 comma 301 minus 26 comma 180 equals 17 comma 121 cm squared
𝑆=253√−25𝜋3≈43,301−26,180=17,121 cm2
✅ Trả lời:
Diện tích phần mặt phẳng giới hạn bởi AB,ACcap A cap B comma cap A cap C
𝐴𝐵,𝐴𝐶
và cung nhỏ BCcap B cap C
𝐵𝐶
xấp xỉ 17,1 cm217 comma 1 cm squared
17,1 cm2
.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104429
Đã trả lời bởi chuyên gia
104429 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69384
Đã trả lời bởi chuyên gia
69384 -
 Đã trả lời bởi chuyên gia
57327
Đã trả lời bởi chuyên gia
57327 -
 Đã trả lời bởi chuyên gia
47948
Đã trả lời bởi chuyên gia
47948 -
 Đã trả lời bởi chuyên gia
45936
Đã trả lời bởi chuyên gia
45936 -
 Đã trả lời bởi chuyên gia
37326
Đã trả lời bởi chuyên gia
37326 -
 Đã trả lời bởi chuyên gia
36237
Đã trả lời bởi chuyên gia
36237


