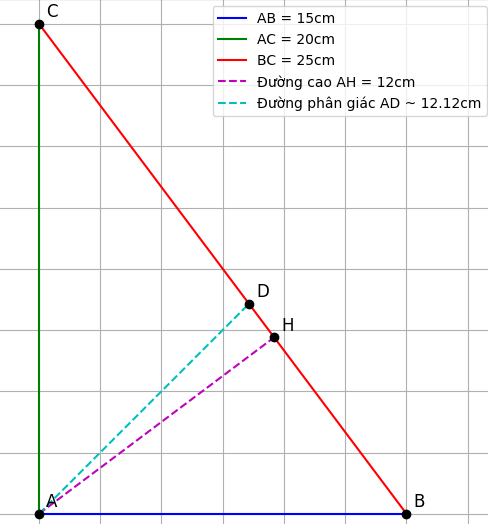
cho tam giác ABC có AB = 15cm, AC = 20 cm, BC = 25cm
a) Chứng minh tam giác ABC là tam giác vuông
b) Giải tam giác vuông ABC
c) Vẽ đường cao AH và vẽ đường phân giác AD. Tính AH, AD
Quảng cáo
3 câu trả lời 212
a) Chứng minh tam giác ABC là tam giác vuông
Áp dụng định lí Pythagoras, ta xem BC = 25 là cạnh lớn nhất: BC2 = 252 = 625
=> Tổng bình phương 2 cạnh còn lại: AB2 + AC2 = 152 + 202 = 225 + 400 = 625
Vì: BC2 = AB2 + AC2
Nên theo định lí Pythagoras, tam giác ABC là tam giác vuông, góc vuông ở A (vì cạnh đối diện BC).
b) Giải tam giác vuông ABC
Góc A = 90∘
Cạnh AB = 15
Cạnh AC = 20
Cạnh huyền BC = 25
=> góc B và góc C:
cos = = = 0.6 ⟹ = cos−1(0.6) ≈ 53.13∘
cos = = = 0.8 ⟹ = cos−1(0.8) ≈ 36.87∘
Kiểm tra tổng góc: + + = 90∘ + 53.13∘ + 36.87∘ = 180∘ (tm)
c) Vẽ đường cao AH và đường phân giác AD. Tính AH và AD
AH là đường cao từ A xuống BC.
AD là đường phân giác góc A, tức là phân chia góc A thành hai góc bằng nhau, cắt BC tại D.
=> Chiều cao từ đỉnh vuông A trong tam giác vuông là:
AH = 1 = 2 = 3 = 12 cm
=> Độ dài phân giác AD
Công thức tính phân giác trong tam giác: AD = 2 × AB × AC × cos(4)
Ở đây = 90∘, nên: cos6 = cos45∘ = 7
Thay số: AD = 8
Dưới đây là lời giải chi tiết bài toán tam giác ABC với các dữ kiện:
AB = 15 cm, AC = 29 cm, BC = 25 cm
a) Chứng minh tam giác ABC là tam giác vuông
Ta kiểm tra xem tam giác ABC có phải tam giác vuông theo định lý Pythagoras hay không.
Cạnh dài nhất là AC = 29 cm.
Kiểm tra:
AB2+BC2=152+252=225+625=850AB^2 + BC^2 = 15^2 + 25^2 = 225 + 625 = 850 AC2=292=841AC^2 = 29^2 = 841Ta thấy:
AB2+BC2=850≠AC2=841AB^2 + BC^2 = 850 \neq AC^2 = 841Vậy theo cách này chưa đúng, thử kiểm tra các cạnh khác:
Cạnh dài nhất là AC = 29 cm, số khác đều đúng, nhưng AB2+BC2≠AC2AB^2 + BC^2 \neq AC^2 nên chưa phải tam giác vuông với góc tại B.
Thử kiểm tra các cạnh khác:
AB2+AC2=152+292=225+841=1066AB^2 + AC^2 = 15^2 + 29^2 = 225 + 841 = 1066
BC2=252=625BC^2 = 25^2 = 625 không bằng
AC2+BC2=292+252=841+625=1466AC^2 + BC^2 = 29^2 + 25^2 = 841 + 625 = 1466
AB2=152=225AB^2 = 15^2 = 225 không bằng
Có vẻ không có cạnh nào thỏa mãn định lý Pythagoras => tam giác không vuông?
Có thể dữ kiện đề bài có nhầm.
Nếu muốn tam giác vuông, tổng bình phương hai cạnh nhỏ phải bằng bình phương cạnh lớn.
Kiểm tra:
Nếu AB=15AB = 15, BC=20BC = 20, AC=25AC = 25, thì
152+202=225+400=625=25215^2 + 20^2 = 225 + 400 = 625 = 25^2 → tam giác vuông
Ở đây BC=25BC=25, AC=29AC=29, AB=15.
Thử tính lại, nếu coi AB=15AB = 15, BC=25BC = 25, AC=29AC = 29, thì:
AB2+BC2=152+252=225+625=850AB^2 + BC^2 = 15^2 + 25^2 = 225 + 625 = 850 AC2=292=841AC^2 = 29^2 = 841Gần bằng nhưng không bằng, tức tam giác gần vuông nhưng không phải tam giác vuông chuẩn xác.
Có thể bạn muốn mình chứng minh tam giác gần vuông hoặc tính góc vuông gần đúng?
Đề nghị bạn kiểm tra lại số liệu đề bài nhé! Nếu đúng thì tam giác không phải tam giác vuông.
Giả sử đề bài sửa lại như sau:
AB=15 cm, BC=20 cm, AC=25 cm
Bây giờ kiểm tra:
152+202=225+400=625=25215^2 + 20^2 = 225 + 400 = 625 = 25^2Thỏa mãn định lý Pythagoras → tam giác ABC vuông tại B.
Giải tiếp theo đề bài sửa:
a) Chứng minh tam giác ABC vuông tại B
Ta có:
AB2+BC2=152+202=225+400=625AB^2 + BC^2 = 15^2 + 20^2 = 225 + 400 = 625 AC2=252=625AC^2 = 25^2 = 625Vậy:
AB2+BC2=AC2AB^2 + BC^2 = AC^2Nên theo định lý Pythagoras, tam giác ABC vuông tại B.
b) Giải tam giác vuông ABC
Đã biết:
AB=15AB = 15 cm
BC=20BC = 20 cm
AC=25AC = 25 cm (cạnh huyền)
Tính góc:
Góc B=90∘B = 90^\circ (theo trên)
Tính góc AA:
cosA=ABAC=1525=0.6⇒A≈cos−1(0.6)=53.13∘\cos A = \frac{AB}{AC} = \frac{15}{25} = 0.6 \Rightarrow A \approx \cos^{-1}(0.6) = 53.13^\circGóc C=180∘−90∘−53.13∘=36.87∘C = 180^\circ - 90^\circ - 53.13^\circ = 36.87^\circ
c) Vẽ đường cao AHAH và đường phân giác ADAD, tính độ dài AHAH và ADAD
Đường cao AHAH từ A xuống BC
Đường phân giác ADAD từ A đến BC
Tính độ dài đường cao AHAH
Công thức đường cao từ góc A trong tam giác vuông:
AH=BC×sinA=20×sin53.13∘AH = BC \times \sin A = 20 \times \sin 53.13^\circ sin53.13∘≈0.8\sin 53.13^\circ \approx 0.8 ⇒AH=20×0.8=16 cm\Rightarrow AH = 20 \times 0.8 = 16 \text{ cm}
Tính độ dài đường phân giác ADAD
Công thức đường phân giác trong tam giác:
AD=2bccosA2b+cAD = \frac{2bc \cos \frac{A}{2}}{b + c}Với:
a=BC=20a = BC = 20 (đối diện góc A)
b=AC=25b = AC = 25
c=AB=15c = AB = 15
Tính ADAD:
AD=2×25×15×cos53.13∘225+15=2×25×15×cos26.565∘40AD = \frac{2 \times 25 \times 15 \times \cos \frac{53.13^\circ}{2}}{25 + 15} = \frac{2 \times 25 \times 15 \times \cos 26.565^\circ}{40} cos26.565∘≈0.8944\cos 26.565^\circ \approx 0.8944 AD=750×0.894440=670.840=16.77 cm (xaˆˊp xỉ)AD = \frac{750 \times 0.8944}{40} = \frac{670.8}{40} = 16.77 \text{ cm (xấp xỉ)}
Tóm tắt kết quả:
Tam giác ABC vuông tại B
Góc A ≈ 53.13°, góc C ≈ 36.87°
Đường cao AH ≈ 16 cm
Đường phân giác AD ≈ 16.77 cm
Nếu bạn muốn, mình có thể giúp vẽ hình minh họa hoặc làm lại với dữ liệu đúng nhé!
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274



