Tìm GTLN-NN của
D = x + x + 1/ x
Quảng cáo
2 câu trả lời 150
- Điều kiện xác định: Trong biểu thức có , nên điều kiện là: x > 0
- Đặt t = ⇒ x = t2, t > 0
Biểu thức trở thành: D = t2 + t +
=> Tìm GTLN, GTNN của D(t) = t2 + t + , với t > 0
=> Tìm đạo hàm: D′(t) = 2t + 1 −
Cho D′(t) = 0 để tìm điểm cực trị: 2t + 1− = 0
⇒ 2t3 + t2 − 1 = 0 : Đây là phương trình bậc ba:
- Thử nghiệm nghiệm bằng cách thử các giá trị nhỏ:
t = 0.5 ⇒ 2(0.5)3 + (0.5)2 − 1 = −0.5
t = 1 ⇒ 2 + 1 − 1 = 2
t = 0.75 ⇒ 2(0.422) + 0.5625 − 1 ≈ 0.4065
t ≈ 0.6 ⇒ thử tiếp sẽ tìm nghiệm gần đúng.
Nhưng ta không cần giải chính xác phương trình bậc 3 để tìm GTLN – GTNN, vì:
+ Xét giới hạn để tìm GTLN và GTNN
Ta phân tích giới hạn của D(t) = t2 + t + :
- Khi t → 0 +: t2 → 0 , t → 0, → +∞ => D(t) → +∞
- Khi t → +∞: t2 → +∞, t → +∞ , → 0 => D(t) → +∞
=> Kết luận: Biểu thức không có giá trị lớn nhất, vì D → +∞ ở cả hai phía.
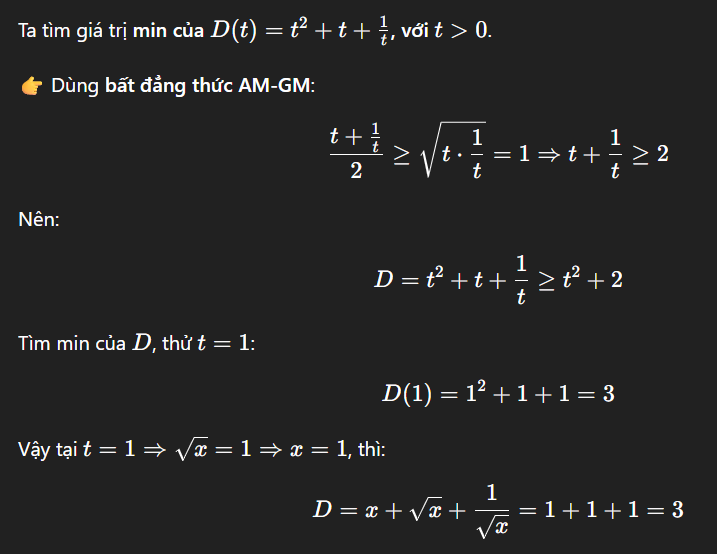
Vậy GTNN của phương trình là 3 tại x = 1, và không có GTLN.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211


