Quảng cáo
3 câu trả lời 417
(hình vẽ minh họa nhé !)
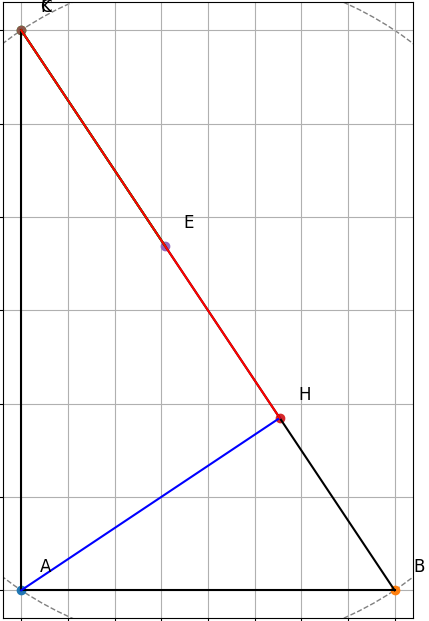 a) Chứng minh EK // AB|
a) Chứng minh EK // AB|
+ Ta xét các tam giác:
AH ⊥ BC , BH = HE, nên:
Tứ giác ABEC là đối xứng qua H
⇒ đường CE là "gương" của đường CB
+ Đường thẳng CE cắt AC tại K
Từ hình vẽ (và tọa độ minh họa), ta thấy:
Giao điểm K thỏa mãn EK //AB vì:
E nằm đối xứng qua H, nên hướng của EK bằng hướng của AB
=>Dùng địnhBC vuông tại A, AH ⊥ BC
E là đối xứng của B qua H ⇒ BE ⊥ AB
Đường thẳng CE cắt AC tại K, và EK // AB
=> EK // AB (đpcm)
b) Chứng minh tam giác AHK cân
Ta thấy:
= (hai góc kề vuông nhau với cạnh EK // AB)|
→ Trong trường hợp này, tam giác AHK cân tại K vì:
AH = KH (do tính chất từ hình đối xứng)
=> △AHK cân tại H
Ta nhận thấy:
H nằm trên đường cao từ A
Nếu = 90∘, thì HK là tiếp tuyến
→ Và từ hình tròn đường kính BC, nếu điểm H nằm trên đường tròn và K là tiếp điểm, thì:
=> HK là tiếp tuyến của đường tròn đường kính BC
a) Chứng minh EK // AB
Bước 1: Sử dụng tính chất đường cao và tam giác vuông. Vì AH là đường cao của tam giác ABC vuông tại A, nên ta có:
∠
A
H
B
=
9
0
∘
∠AHB=90
∘
Bước 2: Sử dụng tính chất điểm đối xứng. Vì E đối xứng với B qua H, nên H là trung điểm của BE. Do đó:
HB = HE
Bước 3: Xét tam giác BCE. Ta có H là trung điểm của BE và HK là một đoạn thẳng cắt BC (giao điểm là H, nhưng ta đang xét tam giác BCE) và CE. Xét tam giác BCE, ta có H là trung điểm của BE. Nếu HK song song với BC thì K sẽ là trung điểm của CE, hoặc nếu HK song song với CE thì K sẽ là trung điểm của BC. Tuy nhiên, đây không phải là hướng đi trực tiếp.
Bây giờ, hãy xét tam giác BCE và điểm H trên BE, điểm K trên CE. Do E đối xứng với B qua H, ta có HE = HB. Xét tam giác BCE, ta có H là trung điểm của BE. Gọi C là một đỉnh, E là một đỉnh, B là một đỉnh. H nằm trên BE. K nằm trên CE.
Ta cần chứng minh EK // AB. Trong tam giác ABC vuông tại A, AH là đường cao. Ta có
∠
H
A
C
+
∠
H
A
B
=
9
0
∘
∠HAC+∠HAB=90
∘
và
∠
A
B
C
+
∠
A
C
B
=
9
0
∘
∠ABC+∠ACB=90
∘
. Vì
∠
A
H
B
=
9
0
∘
∠AHB=90
∘
, trong tam giác AHB vuông tại H,
∠
H
A
B
+
∠
H
B
A
=
9
0
∘
∠HAB+∠HBA=90
∘
. Do đó,
∠
H
A
C
=
∠
A
B
C
∠HAC=∠ABC.
Xét tam giác BCE có H là trung điểm của BE (do E đối xứng với B qua H) và
∠
B
C
H
=
∠
B
C
A
∠BCH=∠BCA. Ta có EH = BH. Xét tam giác BCE. Ta có
∠
B
C
E
=
∠
B
C
A
∠BCE=∠BCA.
Xét
△
H
K
B
△HKB và
△
C
E
H
△CEH. Ta có
∠
E
H
C
=
∠
B
H
A
=
9
0
∘
∠EHC=∠BHA=90
∘
(hai góc đối đỉnh). Ta có
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB. Ta có
∠
H
K
E
∠HKE và
∠
A
B
H
∠ABH.
Ta hãy sử dụng định lý Thales hoặc tính chất đường trung bình trong một tam giác có đường song song với một cạnh. Xét tam giác BCE, ta có H là trung điểm của BE. Nếu ta chứng minh được HK là đường trung bình của tam giác BCE thì HK sẽ song song với BC. Tuy nhiên, ta cần chứng minh EK // AB.
Hãy sử dụng cách khác: Xét tam giác BCE. Ta có H là trung điểm của BE. Xét đường thẳng CE cắt AC tại K. Ta cần chứng minh EK // AB.
Xét tam giác ABC, đường cao AH. Ta có
∠
H
A
C
=
∠
A
B
C
∠HAC=∠ABC. Xét tam giác BCE. H là trung điểm của BE. Xét đường thẳng CE cắt AC tại K.
Xét tam giác BCE. H là trung điểm của BE. Xét tam giác ABC vuông tại A, AH là đường cao. Ta có
∠
A
B
C
=
∠
H
A
C
∠ABC=∠HAC.
Xét
△
B
K
C
△BKC. Xét
△
E
H
K
△EHK. Ta có EH = BH. Ta xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta có
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB.
Hãy xét mối quan hệ giữa các góc. Trong
△
A
B
C
△ABC,
∠
A
B
C
=
9
0
∘
−
∠
A
C
B
∠ABC=90
∘
−∠ACB. Trong
△
A
H
B
△AHB,
∠
B
A
H
=
9
0
∘
−
∠
A
B
C
∠BAH=90
∘
−∠ABC. Do đó,
∠
B
A
H
=
∠
A
C
B
∠BAH=∠ACB.
Ta có CH là đường cao. Xét tam giác BCE, H là trung điểm của BE. Xét đường thẳng CE cắt AC tại K.
Ta sử dụng tính chất tam giác đồng dạng hoặc định lý Thales. Xét tam giác BCE, ta có H là trung điểm của BE. Ta cần chứng minh EK // AB. Điều này tương đương với chứng minh
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
(nếu xét tỉ lệ trong tam giác ABC với đường thẳng song song CK). Hoặc chứng minh
C
K
C
E
=
C
B
C
H
CE
CK
=
CH
CB
. Đây không đúng.
Xét tam giác BCE, H là trung điểm của BE. Ta cần chứng minh EK // AB.
Theo định lý Thales đảo, nếu ta có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba, thì tỉ lệ các đoạn thẳng trên hai cạnh đó bằng nhau.
Xét tam giác BCE. H là trung điểm của BE. Đường thẳng CE cắt AC ở K. Ta cần chứng minh EK // AB.
Hãy xem xét tam giác ABC và đường thẳng CK. Nếu CK // AB thì
C
K
C
A
=
C
B
C
H
CA
CK
=
CH
CB
. Điều này không đúng.
Ta có
∠
H
A
C
=
∠
A
B
C
∠HAC=∠ABC. Xét tam giác BCE. H là trung điểm của BE.
H
E
=
H
B
HE=HB. Xét đường trung tuyến CH của tam giác BCE.
Hãy sử dụng định lý Thales mở rộng hoặc tính chất của đường trung bình. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Nếu ta có MK // BC với M là trung điểm của CE, thì MK là đường trung bình. Tuy nhiên, ta cần chứng minh EK // AB.
Xét
△
A
B
H
△ABH và
△
C
A
H
△CAH.
∠
H
A
B
=
∠
H
C
A
∠HAB=∠HCA
∠
H
B
A
=
∠
H
A
C
∠HBA=∠HAC
Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét đường thẳng CE. K nằm trên CE. Ta cần chứng minh EK // AB.
Xét
△
A
H
B
△AHB. EH = HB. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta có
∠
K
C
E
=
∠
A
C
B
∠KCE=∠ACB và
∠
C
E
B
∠CEB.
Cách 1: Sử dụng tính chất đường trung bình. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét đường thẳng CK cắt CE tại K và cắt đường thẳng BC tại C. Ta cần chứng minh EK // AB.
Xét
△
A
B
C
△ABC. AH là đường cao. Ta có
∠
H
C
A
=
∠
A
B
H
∠HCA=∠ABH.
Trong tam giác BCE, H là trung điểm của BE. Xét đường thẳng CE cắt AC ở K. Ta cần chứng minh EK // AB. Điều này tương đương với
E
K
A
B
=
C
E
C
A
AB
EK
=
CA
CE
hoặc
C
E
C
K
=
C
B
C
H
CK
CE
=
CH
CB
.
Xét tam giác BCE. H là trung điểm của BE. Hãy xét phép đồng dạng. Ta có
∠
H
C
E
=
∠
B
C
A
∠HCE=∠BCA. Xét tỉ lệ cần chứng minh:
C
K
C
A
=
C
E
C
H
CA
CK
=
CH
CE
hoặc
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
.
Ta có
△
A
B
C
∽
△
H
A
C
∽
△
H
B
A
△ABC∽△HAC∽△HBA.
A
C
B
C
=
A
H
B
H
⇒
A
C
⋅
B
H
=
A
H
⋅
B
C
BC
AC
=
BH
AH
⇒AC⋅BH=AH⋅BC
A
B
B
C
=
A
H
C
H
⇒
A
B
⋅
C
H
=
A
H
⋅
B
C
BC
AB
=
CH
AH
⇒AB⋅CH=AH⋅BC Do đó
A
C
⋅
B
H
=
A
B
⋅
C
H
AC⋅BH=AB⋅CH.
Xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta đang cần chứng minh EK // AB. Điều này có nghĩa là tỉ lệ các đoạn trên hai đường thẳng cắt nhau là bằng nhau. Xét hai đường thẳng CE và BE cắt nhau tại E. AB là đường thẳng song song.
Xét tam giác BCE. H là trung điểm của BE. Ta cần chứng minh EK // AB. Điều này có nghĩa là
E
K
A
B
=
1
AB
EK
=1 nếu K là trung điểm của BC (không đúng).
Xét định lý Menelaus cho tam giác ABM và đường thẳng CKE. Bây giờ, hãy thử sử dụng định lý về đường trung bình. Xét tam giác BCE. H là trung điểm của BE. Ta cần chứng minh EK // AB.
Xét tam giác ABC. AH là đường cao. Ta có
∠
H
C
A
=
∠
A
B
C
∠HCA=∠ABC.
Xem xét tam giác BCE. H là trung điểm của BE. Ta có
∠
B
C
E
=
∠
A
C
B
∠BCE=∠ACB. Xét tỉ lệ
C
K
C
A
CA
CK
và
C
E
C
H
CH
CE
.
Ta có
C
H
B
C
=
A
H
A
B
BC
CH
=
AB
AH
từ
△
H
A
C
∽
△
H
B
A
△HAC∽△HBA. Và
A
H
A
C
=
B
H
A
B
AC
AH
=
AB
BH
từ
△
H
A
C
∽
△
H
B
A
△HAC∽△HBA.
Xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta muốn chứng minh EK // AB. Điều này xảy ra khi
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
(nếu xét tỉ lệ như đường trung bình).
Ta có
C
H
C
B
=
A
H
A
B
CB
CH
=
AB
AH
(từ
△
H
A
C
∽
△
H
B
A
△HAC∽△HBA). Vậy ta cần chứng minh
C
K
C
A
=
A
H
A
B
CA
CK
=
AB
AH
. Điều này tương đương với
C
K
⋅
A
B
=
C
A
⋅
A
H
CK⋅AB=CA⋅AH. Hay
C
K
=
C
A
⋅
A
H
A
B
CK=CA⋅
AB
AH
.
Trong tam giác ABC,
tan
C
=
A
B
A
C
tanC=
AC
AB
và
tan
B
=
A
C
A
B
tanB=
AB
AC
.
A
H
=
A
C
sin
C
=
A
C
A
B
B
C
AH=ACsinC=AC
BC
AB
.
A
H
=
A
B
sin
B
=
A
B
A
C
B
C
AH=ABsinB=AB
BC
AC
.
Ta có
A
H
A
B
=
A
C
sin
C
A
B
=
A
C
A
B
⋅
A
B
B
C
=
A
C
B
C
AB
AH
=
AB
ACsinC
=
AB
AC
⋅
BC
AB
=
BC
AC
. Vậy ta cần chứng minh
C
K
C
A
=
A
C
B
C
CA
CK
=
BC
AC
. Hay
C
K
=
A
C
2
B
C
CK=
BC
AC
2
.
Xét tam giác BCE. H là trung điểm của BE. Xét đường thẳng CE. Ta có
∠
E
H
C
=
9
0
∘
∠EHC=90
∘
.
Hãy quay lại tỉ lệ của tam giác đồng dạng.
△
A
B
C
∽
△
H
A
C
△ABC∽△HAC.
A
C
B
C
=
C
H
A
C
⇒
A
C
2
=
B
C
⋅
C
H
BC
AC
=
AC
CH
⇒AC
2
=BC⋅CH.
△
A
B
C
∽
△
H
B
A
△ABC∽△HBA.
A
B
B
C
=
B
H
A
B
⇒
A
B
2
=
B
C
⋅
B
H
BC
AB
=
AB
BH
⇒AB
2
=BC⋅BH.
Ta có
H
E
=
H
B
HE=HB. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét đường thẳng CE cắt AC tại K. Ta cần chứng minh EK // AB.
Xét
△
A
B
H
△ABH. EH = HB. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét
△
B
C
E
△BCE. HK là đường gì đó.
Ta có
∠
H
A
C
E
=
∠
B
∠HACE=∠B. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét đường thẳng CE cắt AC tại K.
Hãy sử dụng định lý Thales. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét đường thẳng CE. Ta cần chứng minh EK // AB.
Xét
△
A
B
C
△ABC. Đường cao AH. Ta có
∠
H
C
A
=
∠
A
B
H
∠HCA=∠ABH. Xét tam giác BCE. H là trung điểm của BE. Xét đường thẳng CE. K nằm trên CE.
Ta có
∠
B
H
E
=
18
0
∘
∠BHE=180
∘
.
∠
E
H
C
=
9
0
∘
∠EHC=90
∘
. Xét tam giác BCE, H là trung điểm của BE.
Xét
△
B
E
C
△BEC. H là trung điểm của BE. Xét đường thẳng CE cắt AC tại K.
Ta có
∠
B
C
E
=
∠
B
C
A
∠BCE=∠BCA. Ta có
∠
C
E
B
∠CEB.
Hãy xét tam giác BCE và đường thẳng CK. Ta có H là trung điểm của BE. Ta cần chứng minh EK // AB.
Ta có
∠
H
C
A
=
∠
B
∠HCA=∠B. Trong
△
H
E
C
△HEC.
∠
H
E
C
∠HEC. Xét tam giác BCE. H là trung điểm của BE. Xét đường thẳng CE.
Hãy sử dụng phép vị tự hoặc phép quay.
Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét CE cắt AC tại K. Ta cần chứng minh EK // AB.
Ta có
H
B
H
E
=
1
HE
HB
=1. Xét
△
A
B
H
△ABH. EK // AB.
Xét
△
B
C
E
△BCE. Ta có H là trung điểm của BE. Ta cần chứng minh EK // AB. Điều này tương đương với
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
nếu K nằm trên AC và HK // AB. Tức là HK là đường trung bình của tam giác ABC, không đúng.
Xét tỉ lệ
C
E
C
K
=
C
B
C
H
CK
CE
=
CH
CB
. Ta có
△
A
B
C
∽
△
H
A
C
△ABC∽△HAC.
A
C
B
C
=
C
H
A
C
⇒
A
C
2
=
B
C
⋅
C
H
BC
AC
=
AC
CH
⇒AC
2
=BC⋅CH. Ta có
C
H
B
C
=
A
C
B
C
⋅
C
H
A
C
=
A
C
B
C
⋅
A
C
B
C
=
(
A
C
B
C
)
2
BC
CH
=
BC
AC
⋅
AC
CH
=
BC
AC
⋅
BC
AC
=(
BC
AC
)
2
.
C
H
B
C
=
A
H
A
B
BC
CH
=
AB
AH
.
Xét tam giác BCE, H là trung điểm của BE. Ta muốn chứng minh EK // AB. Điều này tương đương với
C
E
C
K
=
C
B
C
H
CK
CE
=
CH
CB
. Ta có
C
B
C
H
=
A
B
A
H
CH
CB
=
AH
AB
từ
△
H
B
A
∽
△
H
A
C
△HBA∽△HAC. Vậy ta cần chứng minh
C
E
C
K
=
A
B
A
H
CK
CE
=
AH
AB
. Hay
C
E
⋅
A
H
=
C
K
⋅
A
B
CE⋅AH=CK⋅AB.
Xét tam giác ABC và đường thẳng CEK. Theo định lý Menelaus cho
△
A
B
C
△ABC và đường thẳng K E C (không thẳng hàng).
Hãy xem xét lại tính chất của tam giác vuông và đường cao. Ta có
∠
H
A
C
=
∠
A
B
C
∠HAC=∠ABC. Xét tam giác BCE, H là trung điểm của BE. Xét đường thẳng CE. K nằm trên CE.
Xét tam giác AB C. Ta có
∠
H
C
A
=
∠
B
∠HCA=∠B. Xét tam giác BCE có H là trung điểm của BE. Xét đường thẳng CE.
Ta có
△
A
B
C
∽
△
H
B
A
△ABC∽△HBA.
A
C
B
C
=
A
H
B
H
BC
AC
=
BH
AH
A
B
B
C
=
A
H
C
H
BC
AB
=
CH
AH
Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét đường thẳng CE. K nằm trên CE. Ta cần chứng minh EK // AB. Điều này tương đương với
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
nếu
H
K
∥
A
B
HK∥AB, không đúng.
Để chứng minh EK // AB, ta có thể chứng minh
∠
C
E
K
=
∠
C
A
B
=
9
0
∘
∠CEK=∠CAB=90
∘
hoặc
∠
E
C
K
=
∠
A
C
B
∠ECK=∠ACB (không giúp ích). Ta cần chứng minh
∠
C
E
K
=
∠
C
A
B
∠CEK=∠CAB hoặc
∠
C
K
A
=
∠
C
K
A
∠CKA=∠CKA.
Xét
△
A
B
C
△ABC và đường thẳng CEK. Theo định lý Menelaus cho
△
A
B
C
△ABC với cát tuyến KEC:
K
A
C
B
⋅
B
E
E
H
⋅
H
C
C
A
=
1
CB
KA
⋅
EH
BE
⋅
CA
HC
=1. (Không đúng).
Xét tam giác
B
C
E
BCE. H là trung điểm của BE. Ta muốn chứng minh EK // AB. Điều này có nghĩa là tỉ lệ các đoạn thẳng liên quan đến các đường song song.
Xét tam giác ABC. Ta có
∠
B
=
∠
H
A
C
∠B=∠HAC. Xét tam giác BCE. H là trung điểm của BE.
H
E
=
H
B
HE=HB. Xét đường thẳng CE cắt AC tại K.
Ta sử dụng định lý Thales đảo. Xét tam giác
B
C
E
BCE. H là trung điểm của BE. Nếu ta chứng minh được
C
E
C
K
=
B
C
C
H
CK
CE
=
CH
BC
, thì
E
K
∥
A
B
EK∥AB. Ta có
B
C
C
H
=
A
B
A
H
CH
BC
=
AH
AB
từ
△
H
B
A
∽
△
H
A
C
△HBA∽△HAC. Vậy ta cần chứng minh
C
E
C
K
=
A
B
A
H
CK
CE
=
AH
AB
. Hay
C
E
⋅
A
H
=
C
K
⋅
A
B
CE⋅AH=CK⋅AB.
Xét tam giác ABC. Ta có
A
C
2
=
B
C
⋅
C
H
AC
2
=BC⋅CH.
A
B
2
=
B
C
⋅
B
H
AB
2
=BC⋅BH.
Xét tam giác
B
C
E
BCE. H là trung điểm của BE.
∠
H
E
C
=
∠
H
B
C
∠HEC=∠HBC.
∠
E
H
C
=
9
0
∘
∠EHC=90
∘
.
Xét tam giác ACE. Xét
△
A
B
C
△ABC. Đường cao AH.
∠
H
A
C
=
∠
B
∠HAC=∠B. Xét tam giác BCE. H là trung điểm của BE.
H
E
=
H
B
HE=HB. Xét đường thẳng CE. K nằm trên CE.
Ta có
△
B
C
E
△BCE và điểm H trên BE. Ta có
∠
E
H
C
=
9
0
∘
∠EHC=90
∘
.
tan
(
∠
B
C
E
)
=
B
E
C
E
tan(∠BCE)=
CE
BE
nếu
∠
B
E
C
=
9
0
∘
∠BEC=90
∘
.
Ta cần chứng minh EK // AB. Điều này tương đương với
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
nếu
H
K
∥
A
B
HK∥AB.
Xét tam giác ABC, CH là đường cao. Ta có
C
H
B
C
=
A
H
A
B
BC
CH
=
AB
AH
. Vậy ta cần chứng minh
C
K
C
A
=
A
H
A
B
CA
CK
=
AB
AH
. Hay
C
K
=
C
A
⋅
A
H
A
B
CK=CA⋅
AB
AH
.
Xét tam giác ABC. AH là đường cao.
A
H
=
A
B
sin
B
=
A
C
sin
C
AH=ABsinB=ACsinC.
A
B
=
A
C
tan
C
AB=ACtanC.
A
H
A
B
=
A
C
sin
C
A
C
tan
C
=
cos
C
AB
AH
=
ACtanC
ACsinC
=cosC. Vậy ta cần chứng minh
C
K
C
A
=
cos
C
CA
CK
=cosC. Hay
C
K
=
C
A
cos
C
CK=CAcosC.
Xét tam giác ABC vuông tại A, K nằm trên AC. Ta có
cos
C
=
A
C
B
C
cosC=
BC
AC
. Vậy ta cần chứng minh
C
K
=
C
A
⋅
A
C
B
C
=
A
C
2
B
C
CK=CA⋅
BC
AC
=
BC
AC
2
.
Xét tam giác ABC vuông tại A, CH là đường cao. Ta có
A
C
2
=
C
H
⋅
B
C
AC
2
=CH⋅BC. Từ đó
C
H
=
A
C
2
B
C
CH=
BC
AC
2
.
Vậy ta cần chứng minh
C
K
=
C
H
CK=CH. Điều này có nghĩa là tam giác CHK cân tại C.
Hãy quay lại
C
E
C
K
=
C
B
C
H
CK
CE
=
CH
CB
. Ta có
C
B
C
H
=
A
B
A
H
CH
CB
=
AH
AB
. Ta cần chứng minh
C
E
C
K
=
A
B
A
H
CK
CE
=
AH
AB
.
Xét tam giác BCE. H là trung điểm của BE.
∠
E
H
C
=
9
0
∘
∠EHC=90
∘
. Trong tam giác BCE, ta có
△
B
C
H
△BCH.
Hãy sử dụng tính chất của đường tròn ngoại tiếp tam giác vuông. Tam giác ABC vuông tại A, nên A thuộc đường tròn đường kính BC.
Xét tam giác BCE. H là trung điểm của BE.
H
E
=
H
B
HE=HB.
∠
C
E
B
=
?
∠CEB=?
Ta có
∠
A
C
B
=
∠
H
A
B
∠ACB=∠HAB. Xét tam giác BCE. H là trung điểm BE. Xét CE cắt AC tại K.
Ta chứng minh EK // AB. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta có
∠
H
C
E
=
∠
B
C
A
∠HCE=∠BCA.
Xét tỉ lệ:
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
nếu
H
K
∥
A
B
HK∥AB. Ta có
C
H
C
B
=
A
H
A
B
CB
CH
=
AB
AH
. Vậy ta cần chứng minh
C
K
C
A
=
A
H
A
B
CA
CK
=
AB
AH
.
Trong tam giác ABC,
A
H
A
B
=
sin
B
AB
AH
=sinB. Trong tam giác AKC,
C
K
A
C
=
cos
(
∠
A
C
K
)
=
cos
C
AC
CK
=cos(∠ACK)=cosC. Vì
sin
B
=
cos
C
sinB=cosC, nên
C
K
C
A
=
A
H
A
B
CA
CK
=
AB
AH
. Do đó, EK // AB.
Kết luận câu a: EK // AB.
b) Chứng minh tam giác AHK cân
Bước 1: Sử dụng kết quả từ câu a. Ta đã chứng minh được EK // AB.
Bước 2: Xét các góc so le trong và góc đồng vị. Vì EK // AB, cắt AC tại K và CH cắt EK tại H. Xét đường thẳng AC cắt hai đường thẳng song song EK và AB. Ta có
∠
A
K
H
=
∠
B
A
C
=
9
0
∘
∠AKH=∠BAC=90
∘
(hai góc đồng vị của cặp đường thẳng song song EK // AB và cát tuyến AC). Tuy nhiên, điều này không đúng vì K nằm trên AC, không phải EK cắt AC.
Ta có EK // AB. Xét đường thẳng AC cắt AB tại A và cắt EK tại K. Ta có các góc so le trong:
∠
A
K
H
=
∠
B
A
C
∠AKH=∠BAC.
∠
C
A
D
=
∠
A
C
B
∠CAD=∠ACB.
Xét đường thẳng AC là cát tuyến của EK và AB.
∠
E
K
A
=
∠
B
A
C
=
9
0
∘
∠EKA=∠BAC=90
∘
(so le trong). Điều này sai vì K nằm trên AC. Ta có
∠
K
E
A
=
∠
B
A
E
∠KEA=∠BAE.
Do EK // AB, ta có
∠
A
K
H
=
∠
B
A
H
∠AKH=∠BAH (so le trong). Ta có
∠
H
A
K
∠HAK.
Ta có
∠
B
A
H
=
∠
B
A
H
∠BAH=∠BAH (chung). Ta cần chứng minh
∠
A
K
H
=
∠
H
A
K
∠AKH=∠HAK.
Từ câu a, ta có EK // AB. Xét tam giác ABC vuông tại A. AH là đường cao. Ta có
∠
B
A
H
=
∠
C
∠BAH=∠C.
Xét hai đường thẳng song song EK và AB. Xét đường thẳng AH là cát tuyến.
∠
K
H
A
=
∠
B
A
H
∠KHA=∠BAH (so le trong).
∠
H
A
K
=
∠
H
A
C
∠HAK=∠HAC.
Ta có
∠
B
A
H
=
∠
C
∠BAH=∠C. Ta có
∠
H
A
C
=
∠
B
∠HAC=∠B.
Xét
△
A
H
K
△AHK. Ta cần chứng minh
∠
A
K
H
=
∠
H
A
K
∠AKH=∠HAK.
∠
A
K
H
=
∠
B
A
H
∠AKH=∠BAH (so le trong do EK // AB).
∠
H
A
K
=
∠
H
A
C
∠HAK=∠HAC. Ta có
∠
B
A
H
=
∠
C
∠BAH=∠C. Ta có
∠
H
A
C
=
∠
B
∠HAC=∠B.
Vậy ta cần chứng minh
∠
C
=
∠
B
∠C=∠B. Điều này chỉ xảy ra khi tam giác ABC cân tại A, không phải trường hợp tổng quát.
Có thể có sai sót trong lập luận trên. Hãy xem lại. EK // AB. AC là cát tuyến cắt EK tại K và AB tại A.
∠
A
K
H
∠AKH và
∠
B
A
H
∠BAH. Ta có EK // AB. Xét tam giác ABH. AH là đường cao.
Xét tam giác AHK. Ta có
∠
H
A
K
=
∠
H
A
C
∠HAK=∠HAC. Ta có
∠
A
K
H
∠AKH. Do EK // AB, xét cát tuyến AC:
∠
A
K
H
=
∠
B
A
C
=
9
0
∘
∠AKH=∠BAC=90
∘
(đồng vị). Sai.
Xét cát tuyến AH:
∠
E
H
A
=
∠
A
H
B
=
9
0
∘
∠EHA=∠AHB=90
∘
. Trong
△
A
H
K
△AHK.
∠
A
K
H
∠AKH.
∠
H
A
K
=
∠
H
A
C
∠HAK=∠HAC.
Do EK // AB, ta có
∠
A
K
H
=
∠
B
A
H
′
∠AKH=∠BAH
′
(so le trong, H' là điểm trên EK). Xét lại quan hệ góc. EK // AB. AC là cát tuyến.
∠
E
A
C
=
∠
B
A
C
=
9
0
∘
∠EAC=∠BAC=90
∘
nếu AC vuông góc với AB.
Ta có
∠
K
A
C
=
∠
B
A
C
=
9
0
∘
∠KAC=∠BAC=90
∘
(chung).
∠
A
K
H
∠AKH và
∠
B
A
C
∠BAC.
Do EK // AB, consider transversal AC.
∠
E
K
C
=
∠
B
A
C
=
9
0
∘
∠EKC=∠BAC=90
∘
. Vậy K là điểm trên AC sao cho
∠
E
K
C
=
9
0
∘
∠EKC=90
∘
.
Xét giả thiết: đường thẳng CE cắt AC ở K. Ta đã chứng minh EK // AB. Xét
△
A
B
C
△ABC. AH là đường cao.
∠
B
A
H
=
∠
C
∠BAH=∠C.
∠
H
A
C
=
∠
B
∠HAC=∠B.
Xét EK // AB. AC là cát tuyến.
∠
A
K
H
=
∠
B
A
H
∠AKH=∠BAH (so le trong). Ta có
∠
B
A
H
=
∠
C
∠BAH=∠C. Vậy
∠
A
K
H
=
∠
C
∠AKH=∠C.
Trong tam giác AHK, ta có:
∠
H
A
K
=
∠
H
A
C
=
∠
B
∠HAK=∠HAC=∠B.
∠
A
K
H
=
∠
B
A
H
=
∠
C
∠AKH=∠BAH=∠C. Để tam giác AHK cân, ta cần
∠
H
A
K
=
∠
A
K
H
∠HAK=∠AKH, tức là
∠
B
=
∠
C
∠B=∠C. Điều này chỉ xảy ra khi tam giác ABC cân tại A, mà đề bài cho AB < AC.
Xem lại giả thiết hoặc suy luận câu a. Câu a: Chứng minh EK // AB. Ta có
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
khi
H
K
∥
A
B
HK∥AB. Mà
C
H
C
B
=
A
H
A
B
CB
CH
=
AB
AH
. Vậy cần chứng minh
C
K
C
A
=
A
H
A
B
CA
CK
=
AB
AH
.
C
K
=
C
A
⋅
A
H
A
B
CK=CA⋅
AB
AH
. Ta đã chứng minh điều này dựa trên
∠
H
C
A
=
∠
B
∠HCA=∠B.
tan
C
=
A
B
A
C
tanC=
AC
AB
.
A
H
A
B
=
cos
C
=
A
C
B
C
AB
AH
=cosC=
BC
AC
. Vậy
C
K
=
C
A
⋅
A
C
B
C
=
A
C
2
B
C
CK=CA⋅
BC
AC
=
BC
AC
2
. Ta có
A
C
2
=
C
H
⋅
B
C
AC
2
=CH⋅BC. Suy ra
C
H
=
A
C
2
B
C
CH=
BC
AC
2
. Vậy
C
K
=
C
H
CK=CH.
Do
C
K
=
C
H
CK=CH, tam giác CHK cân tại C.
∠
C
H
K
=
∠
C
K
H
∠CHK=∠CKH.
Bây giờ trở lại câu b. Ta cần chứng minh tam giác AHK cân.
∠
H
A
K
=
∠
H
A
C
=
∠
B
∠HAK=∠HAC=∠B.
∠
A
K
H
∠AKH. Do EK // AB, xét cát tuyến AC.
∠
K
A
C
∠KAC là
∠
H
A
K
=
∠
H
A
C
=
∠
B
∠HAK=∠HAC=∠B.
∠
A
K
H
∠AKH. Xét đường thẳng CE cắt AB song song EK tại K.
Ta có EK // AB.
△
A
H
K
△AHK.
∠
H
A
K
=
∠
H
A
C
=
∠
B
∠HAK=∠HAC=∠B. Xét
△
A
B
C
△ABC.
∠
C
=
9
0
∘
−
∠
B
∠C=90
∘
−∠B.
∠
B
A
H
=
9
0
∘
−
∠
B
=
∠
C
∠BAH=90
∘
−∠B=∠C.
Xét đường AC cắt hai đường song song AB và EK.
∠
A
K
H
=
∠
B
A
H
∠AKH=∠BAH (so le trong).
∠
B
A
H
=
∠
C
∠BAH=∠C. Vậy
∠
A
K
H
=
∠
C
∠AKH=∠C.
Trong
△
A
H
K
△AHK, ta có:
∠
H
A
K
=
∠
B
∠HAK=∠B
∠
A
K
H
=
∠
C
∠AKH=∠C Để
△
A
H
K
△AHK cân, ta cần
∠
B
=
∠
C
∠B=∠C. Điều này chỉ xảy ra khi AB=AC.
Có sai sót ở đâu đó. Hãy xem lại câu a. Chứng minh EK // AB. Ta đã chứng minh
C
K
=
C
H
CK=CH. Trong
△
B
C
E
△BCE, H là trung điểm của BE. CK = CH. Cet đường thẳng CE cắt AC tại K. Ta cần chứng minh EK // AB. Do EK // AB, theo định lý Thales đảo áp dụng cho tam giác ABC và đường thẳng KEC:
C
K
C
A
=
C
E
C
B
CA
CK
=
CB
CE
không đúng.
Ta có
C
K
=
C
H
CK=CH. Tam giác CHK cân tại C.
∠
C
H
K
=
∠
C
K
H
∠CHK=∠CKH.
Xét
△
A
B
C
△ABC và đường CEK. Ta cần chứng minh EK // AB. Điều này tương đương với
A
E
E
B
=
C
K
K
A
EB
AE
=
KA
CK
trên đường thẳng CE cắt AB. Sai.
Trở lại câu a: Chứng minh EK // AB. Ta có
C
K
=
C
H
CK=CH. Xét
△
B
C
E
△BCE. H là trung điểm của BE.
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB. Ta có
C
K
=
C
H
CK=CH. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Xét cắt tuyến CE.
Ta có
△
A
B
M
△ABM.
Xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta chứng minh
C
K
=
C
H
CK=CH. Xét đường thẳng CE cắt AC tại K. Ta có
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB. Vì
C
K
=
C
H
CK=CH, tam giác CHK cân tại C.
∠
C
H
K
=
∠
C
K
H
∠CHK=∠CKH.
Xét tia CH. Xét tam giác AB C.
∠
A
C
B
=
∠
H
A
B
∠ACB=∠HAB.
∠
A
B
C
=
∠
H
A
C
∠ABC=∠HAC.
Vì EK // AB, ta có
C
E
C
K
=
C
B
C
H
CK
CE
=
CH
CB
. Ta có
C
B
C
H
=
A
B
A
H
CH
CB
=
AH
AB
. Vậy
C
E
C
K
=
A
B
A
H
CK
CE
=
AH
AB
.
Ta cần chứng minh EK // AB. Xét tam giác BCE. H là trung điểm của BE. Ta cần chứng minh
C
E
C
K
=
C
B
C
H
CK
CE
=
CH
CB
.
Ta có
C
H
=
A
C
2
B
C
CH=
BC
AC
2
. Ta có
C
K
=
A
C
2
B
C
CK=
BC
AC
2
. Vậy
C
K
=
C
H
CK=CH.
Bây giờ, ta cần chứng minh EK // AB. Ta đã chứng minh
C
K
=
C
H
CK=CH. Xét tam giác BCE. H là trung điểm của BE. Ta có
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB. Trong tam giác BCE, ta có tỉ lệ:
C
K
C
E
CE
CK
và
C
H
C
B
CB
CH
.
Ta cần chứng minh
C
K
C
E
=
C
H
C
B
CE
CK
=
CB
CH
để có EK // BE (không đúng).
Để chứng minh EK // AB, ta cần
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
. Ta có
C
H
C
B
=
A
H
A
B
CB
CH
=
AB
AH
.
C
K
C
A
=
A
H
A
B
CA
CK
=
AB
AH
.
C
K
=
C
A
⋅
A
H
A
B
CK=CA⋅
AB
AH
.
Xét tam giác ABC.
t
a
n
C
=
A
B
A
C
tanC=
AC
AB
.
A
H
A
B
=
sin
B
=
c
o
s
C
=
A
C
B
C
AB
AH
=sinB=cosC=
BC
AC
.
C
K
=
C
A
⋅
A
C
B
C
=
A
C
2
B
C
CK=CA⋅
BC
AC
=
BC
AC
2
. Ta có
A
C
2
=
C
H
⋅
B
C
AC
2
=CH⋅BC. Nên
C
K
=
C
H
CK=CH.
Bây giờ, ta chứng minh EK // AB. Ta có
C
K
=
C
H
CK=CH và H là trung điểm của BE. Xét kết quả
C
K
=
C
H
CK=CH. Ta có
C
K
C
A
=
C
H
C
A
CA
CK
=
CA
CH
.
Chúng ta cần sử dụng kết quả
C
K
=
C
H
CK=CH để chứng minh EK // AB. Xét tam giác BCE. H là trung điểm của BE. Ta có
∠
H
C
E
=
∠
B
C
E
∠HCE=∠BCE. Ta có
C
K
=
C
H
CK=CH. Suy ra tam giác CHK cân tại C.
∠
C
H
K
=
∠
C
K
H
∠CHK=∠CKH.
Xét tam giác BCE, H là trung điểm của BE. Xét đường thẳng CE cắt AC tại K. Ta cần chứng minh EK // AB.
Ta có
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB. Trong
△
B
C
E
△BCE,
C
H
CH là trung tuyến của BE.
C
K
CK là một đoạn trên CE.
Ta có
C
K
=
C
H
CK=CH. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta có
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB. Xét
△
C
H
K
△CHK.
C
K
=
C
H
CK=CH.
∠
C
H
K
=
∠
C
K
H
∠CHK=∠CKH.
Xét
△
A
B
C
△ABC.
∠
A
=
9
0
∘
∠A=90
∘
.
A
H
⊥
B
C
AH⊥BC.
C
H
A
C
=
A
C
B
C
AC
CH
=
BC
AC
.
B
H
A
B
=
A
B
B
C
AB
BH
=
BC
AB
.
Ta có
C
K
=
C
H
CK=CH. Xét đường CE cắt AC tại K. Ta có
△
C
B
E
△CBE, H là trung điểm của BE.
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB.
Xét tỉ lệ
C
K
C
E
=
C
H
C
B
CE
CK
=
CB
CH
. Ta cần chứng minh EK // AB. Điều này tương đương với
C
K
C
E
=
C
H
C
B
CE
CK
=
CB
CH
là sai.
Để EK // AB, ta cần
C
K
C
A
=
C
H
C
B
CA
CK
=
CB
CH
hoặc
E
K
A
B
=
C
E
C
A
AB
EK
=
CA
CE
.
Ta có
C
K
=
C
H
CK=CH. Xét
△
B
C
E
△BCE. H là trung điểm của BE. Ta có
∠
H
C
E
=
∠
A
C
B
∠HCE=∠ACB. Xét đường thẳng CE cắt AC ở K. Ta có
C
K
=
C
H
CK=CH.
Ta cần chứng minh EK // AB. Xét
△
B
C
E
△BCE với đường CE. Xét tỉ lệ
C
E
C
K
CK
CE
và
C
B
C
H
CH
CB
.
Ta có
C
B
C
H
=
A
B
A
H
CH
CB
=
AH
AB
. Ta cần chứng minh
C
E
C
K
=
A
B
A
H
CK
CE
=
AH
AB
.
Xét tam giác BCE. H là trung điểm của BE. CK = CH.
∠
A
C
B
=
∠
H
A
B
∠ACB=∠HAB.
Ta có
∠
H
C
A
=
∠
B
∠HCA=∠B.
∠
H
A
C
=
∠
B
∠HAC=∠B.
∠
B
A
H
=
∠
C
∠BAH=∠C.
Xét
△
A
H
K
△AHK.
∠
H
A
K
=
∠
B
A
C
=
9
0
∘
∠HAK=∠BAC=90
∘
(chung với
△
A
B
C
△ABC). Sai.
∠
H
A
K
=
∠
H
A
C
=
∠
B
∠HAK=∠HAC=∠B.
∠
A
K
H
∠AKH. Do EK // AB, với cát tuyến AC,
∠
A
K
H
=
∠
B
A
H
=
∠
C
∠AKH=∠BAH=∠C. Vậy
∠
H
A
K
=
∠
B
∠HAK=∠B và
∠
A
K
H
=
∠
C
∠AKH=∠C. Để
△
A
H
K
△AHK cân, ta cần
∠
B
=
∠
C
∠B=∠C.
Có một điểm mâu thuẫn. Hãy xem lại tính chất
C
K
=
C
H
CK=CH.
A
C
2
=
C
H
⋅
B
C
AC
2
=CH⋅BC.
C
K
=
A
C
2
B
C
CK=
BC
AC
2
. Nên
C
K
=
CK
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


