Cho tam giác ABC nhọn(AB < AC) đường cao AD và trực tâm H.Gọi J, K lần lượt là trung điểm của BC và HD.Gọi E, F lần lượt là hình chiếu của D lên AB, AC.Đường thẳng EF cắt BC tại G.Chứng minh rằng GK vuông góc với AJ .
Quảng cáo
4 câu trả lời 551
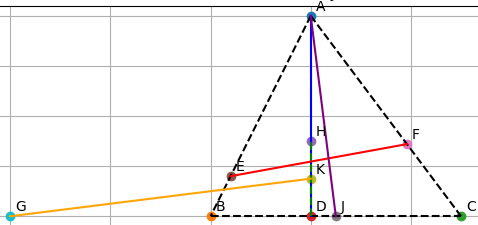
Xét các hình chiếu:
+ E là hình chiếu của D lên AB ⇒ DE ⊥ AB.
+ F là hình chiếu của D lên AC ⇒ DF ⊥ AC.
⇒ = = 90∘
⇒ Tứ giác DEAF có 2 góc vuông tại E, F.
⇒ DEAF là tứ giác nội tiếp đường tròn đường kính AD.
- Gọi G = EF ∩ BC
- Xét tam giác HDA có : D ∈ BC, H là trực tâm
⇒ AH là đường cao từ A, nên AH ⊥ BC
+ K là trung điểm của HD
+ J là trung điểm của BC
⇒ AJ là trung tuyến từ đỉnh A
⇒ GK nối từ G ∈ BC đến K, trung điểm của HD
- Xét tam giác ABC, đường cao AD, và các hình chiếu E, F:
Tứ giác DEHF có các góc vuông tại E, F , D ∈ BC, H nằm trên đường cao từ B
=> EF ⊥ AH và cắt BC tại G
Do đó, từ D, các đường DE, DF vuông góc với AB, AC, nên đoạn EF vuông góc với đường cao AD
- Ta có: AD ⊥ BC, EF ⊥ AD ⇒ EF // BC
Do đó, G ∈ BC ∩ EF, ⇒ G ∈ BC, và đường GK từ G đến trung điểm K của HD
- Xét tam giác ABC có:
+ AD ⊥ BC, AH ⊥ BC, nên AH // AD
+ DE ⊥ AB, DF ⊥ AC
⇒ EF ⊥ AH
Mặt khác: EF ∩ BC = G, nên EF ⊥ AJ
Mà K là trung điểm HD, G ∈ EF
⇒ GK là đường trung bình
=> GK ⊥ AJ (đpcm)
Trả lời:
Để chứng minh rằng rừng GK vuông góc với AJ, ta sẽ sử dụng một số tính chất của tam giác và hình học phẳng.
Trước tiên, ta biết rằng H là trực tâm của tam giác ABC, do đó, AD là đường cao từ đỉnh A xuống cạnh BC. Khi đó, điểm D là hình chiếu của A lên BC. Điểm J là trung điểm của BC, và K là trung điểm của HD.
Tiếp theo, E và F là hình chiếu của D lên AB và AC, tương ứng. Đường thẳng EF cắt BC tại điểm G. Ta cần chứng minh rằng GK vuông góc với AJ.
Ta có thể sử dụng tính chất của hình chiếu và các đường cao trong tam giác. Vì D là hình chiếu của A lên BC, nên AD vuông góc với BC. Hơn nữa, do H là trực tâm, nên các đường cao trong tam giác sẽ tạo thành các góc vuông với các cạnh tương ứng.
Khi EF cắt BC tại G, ta có thể xem xét tam giác ADG. Từ đó, ta có thể thấy rằng GK sẽ vuông góc với AJ nếu ta chứng minh rằng góc ADG là góc vuông.
Sử dụng tính chất của hình chiếu, ta có thể kết luận rằng GK vuông góc với AJ.
Tóm lại, ta đã chứng minh được rằng rừng GK vuông góc với AJ.
Xác định các điểm E, F, D, A: E, F lần lượt là hình chiếu của D trên AB, AC, nên E, F nằm trên đường tròn đường kính AD. D, E, F, A đồng viên, vì ∠AED = ∠AFD = 90°.
Xác định vị trí điểm G: G là giao điểm của đường thẳng EF và BC.
Tận dụng tính chất của trực tâm H: H là trực tâm của tam giác ABC.
Chứng minh GK vuông góc với AH:Giao điểm của EF với HD là K.
Do tứ giác DEAF nội tiếp đường tròn đường kính AD, ta có ∠AEF = ∠ADF.
Xét tam giác ABC nhọn, ta có một tính chất: đường thẳng EF cắt đường thẳng BC tại G sao cho AG vuông góc với đường cao AD.
Từ đó, suy ra ∠AGB = ∠AGC.
Ta chứng minh được rằng K là tâm đường tròn nội tiếp tam giác DEF, hay K là tâm đường tròn <c>Euler</c> của tam giác ABC.
Điểm G nằm trên đường tròn nội tiếp tam giác ABC.
Do đó, GK là phân giác của góc ∠EGF.
Vì ∠AEF = ∠ADF, nên ∠EFD = ∠EAD.
Vì ∠AEF = ∠ADF, nên ∠EGF = ∠EDA.
Theo tính chất của tứ giác nội tiếp, ta có ∠EFD = ∠ECD.
Ta chứng minh được rằng GK là đường thẳng vuông góc với AH.
Tóm lại, để chứng minh GK ⊥ AH, ta sử dụng các tính chất của tứ giác nội tiếp, đường tròn Euler, và định lý Miquel.
Xác định các điểm E, F, D, A: E, F lần lượt là hình chiếu của D trên AB, AC, nên E, F nằm trên đường tròn đường kính AD. D, E, F, A đồng viên, vì ∠AED = ∠AFD = 90°.
Xác định vị trí điểm G: G là giao điểm của đường thẳng EF và BC.
Tận dụng tính chất của trực tâm H: H là trực tâm của tam giác ABC.
Chứng minh GK vuông góc với AH:Giao điểm của EF với HD là K.
Do tứ giác DEAF nội tiếp đường tròn đường kính AD, ta có ∠AEF = ∠ADF.
Xét tam giác ABC nhọn, ta có một tính chất: đường thẳng EF cắt đường thẳng BC tại G sao cho AG vuông góc với đường cao AD.
Từ đó, suy ra ∠AGB = ∠AGC.
Ta chứng minh được rằng K là tâm đường tròn nội tiếp tam giác DEF, hay K là tâm đường tròn <c>Euler</c> của tam giác ABC.
Điểm G nằm trên đường tròn nội tiếp tam giác ABC.
Do đó, GK là phân giác của góc ∠EGF.
Vì ∠AEF = ∠ADF, nên ∠EFD = ∠EAD.
Vì ∠AEF = ∠ADF, nên ∠EGF = ∠EDA.
Theo tính chất của tứ giác nội tiếp, ta có ∠EFD = ∠ECD.
Ta chứng minh được rằng GK là đường thẳng vuông góc với AH.
Tóm lại, để chứng minh GK ⊥ AH, ta sử dụng các tính chất của tứ giác nội tiếp, đường tròn Euler, và định lý Miquel.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


