Kẻ hình và giải giúp em với ạ.Em cảm ơn nhieu lắm ạ
Quảng cáo
3 câu trả lời 468
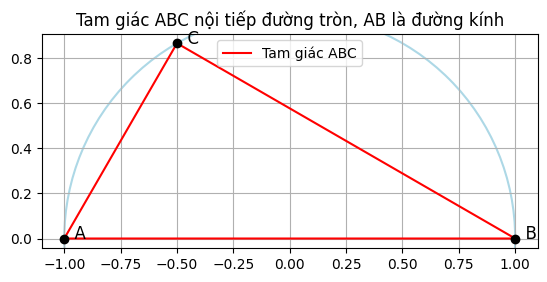
+ Vì AB= là đường kính của đường tròn và điểm C thuộc đường tròn nên theo định lý Thales, tam giác ABC vuông tại C nếu C nằm trên đường tròn sao cho AB là đường kính.
+ Tuy nhiên, ở đây AC = R = AB→ tức là C không nằm đối xứng với B qua O, mà nằm tạo thành một tam giác có:
AB = 2R
AC = R
→ Chứng tỏ △ABC là tam giác vuông tại B
+ Gọi độ dài các cạnh:
Giả sử bán kính đường tròn là R
AB = 2R (vì AB là đường kính)
AC = R (giả thiết)
Dựng điểm C sao cho AC = Rvà C∈(O)
+ Áp dụng định lý cosin để tính góc A:
Trong tam giác ABC, gọi:
a = BC (cạnh đối góc A)
b = AC = R
c = AB = 2R+
=> Tính độ dài cạnh a = BC theo định lý cosin:
Ta có:
AC = R, AB = 2R ⇒Tam giác ABC có các cạnh: AC = R, AB = 2R+
+ Dựa vào hình học hoặc tọa độ, ta có:![]()

+ Đặt hệ trục tọa độ để tính toán dễ hơn:
Gọi A(−R,0), B(R,0), O(0,0)
Gọi C là điểm thuộc đường tròn, sao cho AC = R
Ta chứng minh:
Điểm C = () thỏa mãn:
OC = R (thuộc đường tròn)
AC = R (theo tính toán khoảng cách)
+ Tính các cạnh: AB = 2R, AC = R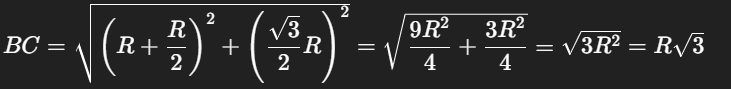
+ Tính các góc bằng định lý cosin:
+) cos() = ![]()
= ![]() => = 60∘
=> = 60∘
+) cos() = ![]()
![]() => = 30∘
=> = 30∘
+) = 180∘ − − =180∘ − 60∘ − 30∘ = 90∘
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


