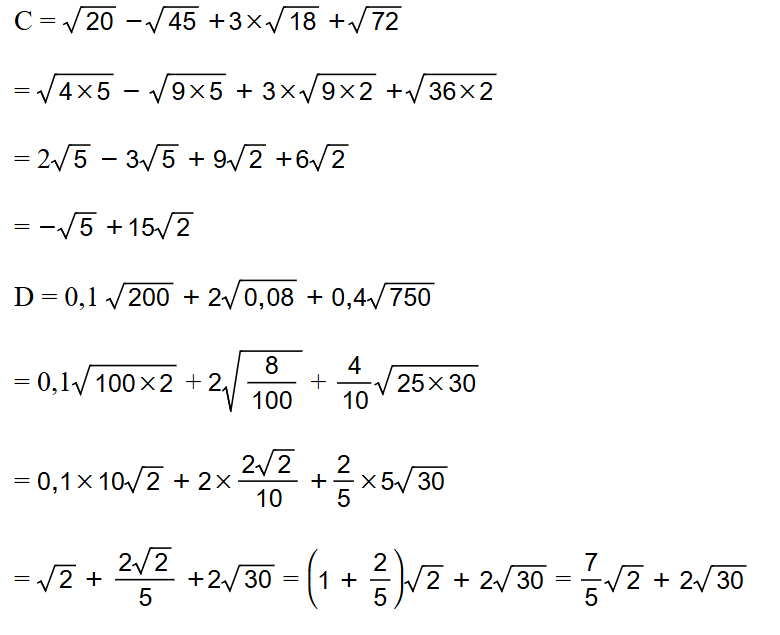Tính :
A= 5 1/5 + 1/2 20 + 5
B = 1/2 + 4,5 + 12,5
C = 20 - 45 + 3 18 + 72
E = 0,1 200 + 2 0,08 + 0,4750
Quảng cáo
4 câu trả lời 251
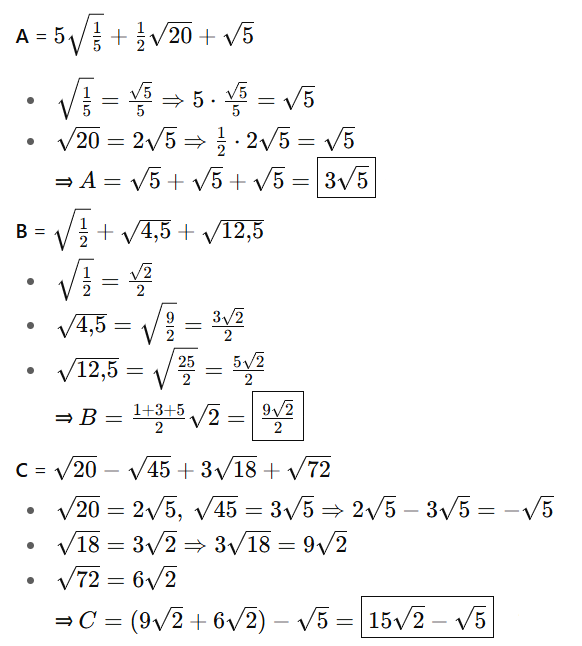 Tớ gửi
Tớ gửi
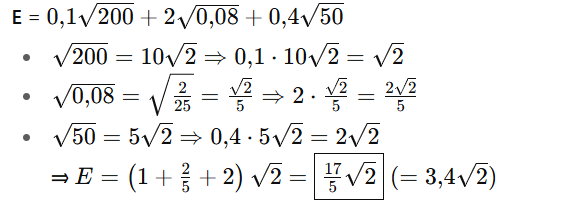 Nốt nè
Nốt nè
Để tính các biểu thức A, B, C, E, chúng ta cần đơn giản hóa từng biểu thức bằng cách xử lý các căn thức và thực hiện các phép tính cần thiết. Dưới đây là lời giải chi tiết:
---
### **1. Tính A = 5√(1/5) + (1/2)√20 + √5**
Bước 1: Đơn giản hóa từng thành phần.
- **5√(1/5)**:
\[
\sqrt{\frac{1}{5}} = \frac{\sqrt{1}}{\sqrt{5}} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5} \quad (\text{sau khi nhân tử và mẫu với } \sqrt{5}).
\]
Do đó:
\[
5 \sqrt{\frac{1}{5}} = 5 \cdot \frac{1}{\sqrt{5}} = \frac{5}{\sqrt{5}} = \sqrt{5} \quad (\text{sau khi nhân tử và mẫu với } \sqrt{5}, \frac{5 \cdot \sqrt{5}}{5} = \sqrt{5}).
\]
- **(1/2)√20**:
\[
\sqrt{20} = \sqrt{4 \cdot 5} = 2\sqrt{5}.
\]
Do đó:
\[
\frac{1}{2} \cdot \sqrt{20} = \frac{1}{2} \cdot 2\sqrt{5} = \sqrt{5}.
\]
- **√5**: Không cần đơn giản hóa.
Bước 2: Cộng các thành phần.
\[
A = \sqrt{5} + \sqrt{5} + \sqrt{5} = 3\sqrt{5}.
\]
**Kết quả: \( A = 3\sqrt{5} \).**
---
### **2. Tính B = √(1/2) + √4.5 + √12.5**
Bước 1: Đơn giản hóa từng thành phần.
- **√(1/2)**:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}.
\]
- **√4.5**:
\[
4.5 = \frac{9}{2}, \quad \sqrt{4.5} = \sqrt{\frac{9}{2}} = \frac{\sqrt{9}}{\sqrt{2}} = \frac{3}{\sqrt{2}} = \frac{3\sqrt{2}}{2}.
\]
- **√12.5**:
\[
12.5 = \frac{25}{2}, \quad \sqrt{12.5} = \sqrt{\frac{25}{2}} = \frac{\sqrt{25}}{\sqrt{2}} = \frac{5}{\sqrt{2}} = \frac{5\sqrt{2}}{2}.
\]
Bước 2: Cộng các thành phần.
\[
B = \frac{\sqrt{2}}{2} + \frac{3\sqrt{2}}{2} + \frac{5\sqrt{2}}{2} = \frac{\sqrt{2} + 3\sqrt{2} + 5\sqrt{2}}{2} = \frac{9\sqrt{2}}{2}.
\]
**Kết quả: \( B = \frac{9\sqrt{2}}{2} \).**
---
### **3. Tính C = √20 - √45 + 3√18 + √72**
Bước 1: Đơn giản hóa từng thành phần.
- **√20**:
\[
\sqrt{20} = \sqrt{4 \cdot 5} = 2\sqrt{5}.
\]
- **√45**:
\[
\sqrt{45} = \sqrt{9 \cdot 5} = 3\sqrt{5}.
\]
- **3√18**:
\[
\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}, \quad 3\sqrt{18} = 3 \cdot 3\sqrt{2} = 9\sqrt{2}.
\]
- **√72**:
\[
\sqrt{72} = \sqrt{36 \cdot 2} = 6\sqrt{2}.
\]
Bước 2: Cộng và trừ các thành phần.
\[
C = 2\sqrt{5} - 3\sqrt{5} + 9\sqrt{2} + 6\sqrt{2}.
\]
Nhóm các số hạng có cùng căn thức:
- Với \(\sqrt{5}\): \(2\sqrt{5} - 3\sqrt{5} = -1\sqrt{5} = -\sqrt{5}\).
- Với \(\sqrt{2}\): \(9\sqrt{2} + 6\sqrt{2} = 15\sqrt{2}\).
Do đó:
\[
C = -\sqrt{5} + 15\sqrt{2}.
\]
**Kết quả: \( C = 15\sqrt{2} - \sqrt{5} \).**
---
### **4. Tính E = 0.1√200 + 2√0.08 + 0.4√50**
Bước 1: Đơn giản hóa từng thành phần.
- **0.1√200**:
\[
\sqrt{200} = \sqrt{100 \cdot 2} = 10\sqrt{2}, \quad 0.1 \cdot \sqrt{200} = 0.1 \cdot 10\sqrt{2} = \sqrt{2}.
\]
- **2√0.08**:
\[
0.08 = \frac{8}{100} = \frac{2}{25}, \quad \sqrt{0.08} = \sqrt{\frac{2}{25}} = \frac{\sqrt{2}}{\sqrt{25}} = \frac{\sqrt{2}}{5}.
\]
Do đó:
\[
2 \cdot \sqrt{0.08} = 2 \cdot \frac{\sqrt{2}}{5} = \frac{2\sqrt{2}}{5}.
\]
- **0.4√50**:
\[
\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}, \quad 0.4 \cdot \sqrt{50} = 0.4 \cdot 5\sqrt{2} = 2\sqrt{2}.
\]
Bước 2: Cộng các thành phần.
\[
E = \sqrt{2} + \frac{2\sqrt{2}}{5} + 2\sqrt{2}.
\]
Nhóm các số hạng:
\[
E = \sqrt{2} + \frac{2\sqrt{2}}{5} + 2\sqrt{2} = \left(1 + \frac{2}{5} + 2\right)\sqrt{2} = \left(\frac{5}{5} + \frac{2}{5} + \frac{10}{5}\right)\sqrt{2} = \frac{17}{5}\sqrt{2}.
\]
**Kết quả: \( E = \frac{17}{5}\sqrt{2} \).**
---
### **Kết quả cuối cùng:**
\[
\boxed{
\begin{aligned}
A &= 3\sqrt{5}, \\
B &= \frac{9\sqrt{2}}{2}, \\
C &= 15\sqrt{2} - \sqrt{5}, \\
E &= \frac{17}{5}\sqrt{2}.
\end{aligned}
}
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490