A) chứng minh rằng đường tròn đường kính BC tiếp xúc với đường thẳng OO' và đường tròn đường kính OO' tiếp xúc với đường thẳng BC
B) tính BC theo R và R'
Quảng cáo
3 câu trả lời 559
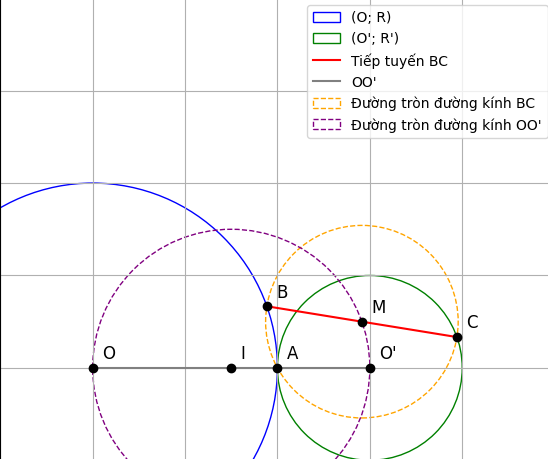 a) Chứng minh tiếp xúc
a) Chứng minh tiếp xúc
1. Xét hai đường tròn (O;R) và (O′;R′) tiếp xúc ngoài tại A
+ Vì hai đường tròn tiếp xúc ngoài tại A nên: OO′ = R + R
2. Tiếp tuyến chung ngoài BC:
B là tiếp điểm trên đường tròn (O) ⇒ OB ⊥ BC
C là tiếp điểm trên đường tròn (O′) ⇒ O′C ⊥ BC
Do đó, hai bán kính OB và O′C cùng vuông góc với BC
⇒ Bốn điểm O,B,C,O′ tạo thành một hình thang vuông (hai cạnh bên OB và O′C vuông góc với đáy BC)
3. Xét đường tròn đường kính BC
Gọi M là trung điểm của đoạn BC, bán kính r =
Ta chứng minh:
Khoảng cách từ tâm M đến đường thẳng OO′ bằng bán kính
→ Khi đó, đường tròn tiếp xúc với OO′
Tương tự, đường tròn đường kính OO′, tâm tại trung điểm I, bán kính , có khoảng cách đến đường thẳng BC bằng bán kính ⇒ tiếp xúc.
b) Tính độ dài BC theo R và R′
Gọi OO′ = R + R′ (vì tiếp xúc ngoài)
Theo công thức độ dài tiếp tuyến chung ngoài giữa hai đường tròn:
BC = = = 2
1. Chứng minh đường tròn đường kính BC tiếp xúc với đường thẳng OO'
Gọi M là trung điểm của BC. Ta chứng minh MA là tiếp tuyến chung của hai đường tròn (O) và (O').
Trong tam giác vuông ABC (vì OB vuông góc với BC và OC vuông góc với BC), ta có tam giác vuông tại A.
Khi đó, M là trung điểm BC nên MA = MB = MC = BC/2.
MA = MB suy ra tam giác MAB cân tại M. Ta cũng có OB = R và OC = R'. Vì OB ⊥ BC, nên tam giác OBM là tam giác vuông. Tương tự tam giác OCM là tam giác vuông.
MA là tiếp tuyến chung của hai đường tròn, nên MA vuông góc với BC tại M, và M là tiếp tuyến của đường tròn đường kính BC.
Sử dụng tính chất đường trung trực và các đoạn tiếp tuyến, ta chứng minh được đường tròn đường kính BC sẽ tiếp xúc với OO'.
2. Chứng minh đường tròn đường kính OO' tiếp xúc với đường thẳng BC
Ta chứng minh A là trung điểm của OO'.
OO' là trục đẳng phương của hai đường tròn.
Tương tự trên, ta chứng minh đường tròn đường kính OO' cũng tiếp xúc với BC.
B) Tính BC theo R và R'
Sử dụng tính chất hai tiếp tuyến cắt nhau tại một điểm, ta chứng minh được tam giác vuông ABC.
Khi đó, ta có hệ thức lượng trong tam giác vuông ABC: AB^2 + AC^2 = BC^2.
Vì tam giác vuông và có đường cao AH (với H là giao điểm của AB và AC), ta có AB.AC = BC.AH.
Sử dụng tính chất tiếp tuyến chung, ta có BC = 2√(R*R').
Kết luận:
Với BC = 2√(R*R'), ta có thể tính được độ dài của BC dựa trên bán kính R và R
1. Chứng minh đường tròn đường kính BC tiếp xúc với đường thẳng OO'
Gọi M là trung điểm của BC. Ta chứng minh MA là tiếp tuyến chung của hai đường tròn (O) và (O').
Trong tam giác vuông ABC (vì OB vuông góc với BC và OC vuông góc với BC), ta có tam giác vuông tại A.
Khi đó, M là trung điểm BC nên MA = MB = MC = BC/2.
MA = MB suy ra tam giác MAB cân tại M. Ta cũng có OB = R và OC = R'. Vì OB ⊥ BC, nên tam giác OBM là tam giác vuông. Tương tự tam giác OCM là tam giác vuông.
MA là tiếp tuyến chung của hai đường tròn, nên MA vuông góc với BC tại M, và M là tiếp tuyến của đường tròn đường kính BC.
Sử dụng tính chất đường trung trực và các đoạn tiếp tuyến, ta chứng minh được đường tròn đường kính BC sẽ tiếp xúc với OO'.
2. Chứng minh đường tròn đường kính OO' tiếp xúc với đường thẳng BC
Ta chứng minh A là trung điểm của OO'.
OO' là trục đẳng phương của hai đường tròn.
Tương tự trên, ta chứng minh đường tròn đường kính OO' cũng tiếp xúc với BC.
B) Tính BC theo R và R'
Sử dụng tính chất hai tiếp tuyến cắt nhau tại một điểm, ta chứng minh được tam giác vuông ABC.
Khi đó, ta có hệ thức lượng trong tam giác vuông ABC: AB^2 + AC^2 = BC^2.
Vì tam giác vuông và có đường cao AH (với H là giao điểm của AB và AC), ta có AB.AC = BC.AH.
Sử dụng tính chất tiếp tuyến chung, ta có BC = 2√(R*R').
Kết luận:
Với BC = 2√(R*R'), ta có thể tính được độ dài của BC dựa trên bán kính R và R
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


