Quảng cáo
4 câu trả lời 668
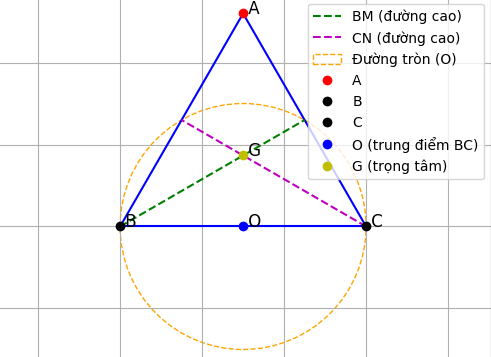
1. Vị trí điểm A so với đường tròn đường kính BC
Vì tam giác ABC đều, nên:
+) AB = BC = CA = a
+) = = = 60∘
Gọi O là trung điểm của BC, suy ra:
O là tâm đường tròn đường kính BC
Bán kính R = =
+ Xét tam giác ABC đều:
Cao từ A xuống BC vuông góc BC tại trung điểm, đồng thời là trung tuyến, phân giác
Gọi H là chân đường cao từ A đến BC
⇒ AH vuông góc BC
Tọa độ hóa để chứng minh vị trí tương đối:
Gán tọa độ: B(0,0), C(a,0) ⇒ O(, 0)
Vì tam giác đều nên chiều cao h = ⇒ A(, )
Phương trình đường tròn tâm O(, 0), bán kính R = : (x − )2 + y2 = ()2
Thế tọa độ A(, ) vào phương trình:
( − )2 + ()2 = 0 + 8 > 9
⇒ A nằm ngoài đường tròn.
BM và CN là các đường cao của tam giác đều
G là giao điểm của hai đường cao ⇒ là trực tâm tam giác ABC
Với tam giác đều, trực tâm trùng trọng tâm và trực giao điểm các trung tuyến.
Gọi G là trọng tâm của tam giác đều ABC
⇒ G có tọa độ:
....
Chứng minh điểm A nằm ngoài đường tròn tâm O đường kính BC
1. Xác định đường tròn:
Đường tròn tâm O có đường kính là BC, nên tâm O là trung điểm của BC và bán kính là R = BC/2 = a/2.
2. Tính khoảng cách AO:
Trong tam giác ABC đều, đường cao BM và CN cũng là đường trung tuyến và phân giác. Điểm A cách BC một khoảng bằng chiều cao của tam giác đều, tức là h = a√3/2.
3. So sánh AO với bán kính:
Khoảng cách AO = h = a√3/2. So với bán kính R = a/2, ta có a√3/2 > a/2, tức là AO > R. Do đó, điểm A nằm ngoài đường tròn tâm O đường kính BC.
Chứng minh điểm G nằm trong đường tròn tâm O đường kính BC
1. Xác định điểm G:
Điểm G là giao điểm của hai đường cao BM và CN, do đó G là trực tâm của tam giác ABC đều.
2. Vị trí của G trong tam giác đều:
Trực tâm của tam giác đều cũng là trọng tâm và tâm đường tròn nội tiếp.
3. Tính khoảng cách OG:
Khoảng cách từ trọng tâm đến trung điểm của cạnh đối diện bằng 1/3 độ dài đường trung tuyến. Trong tam giác đều, trọng tâm G chia đường cao BM theo tỉ lệ BG = 2/3 BM và GM = 1/3 BM. Tương tự, O là trung điểm BC, nên BO = R = a/2.
4. So sánh OG với bán kính:
Điểm G là trọng tâm, O là trung điểm của cạnh BC. Ta có OG là một phần của đường trung tuyến BM. Khoảng cách OG = 1/3 BM. Vì G là trọng tâm và O là trung điểm của BC, nên G nằm gần O hơn đỉnh A, tức là OG < OA. Hơn nữa, khoảng cách từ G đến tâm O là OG = 1/3 BM. Vì BM là đường cao, ta có BM = a√3/2. Suy ra OG = (1/3) * (a√3/2) = a√3/6.
So với bán kính R = a/2, ta có a√3/6 < a/2, tức là OG < R. Do đó, điểm G nằm trong đường tròn tâm O đường kính BC.
nè
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


