a) Chứng minh AC là tiếp tuyến tại C của (O).
b) Từ B vẽ đường thẳng song song với OA; cắt (O) tại D (D khác B). Chứng minh: CD là đường kính của (O).
c) Gọi K là giao điểm thứ hai của AD và (O). Chứng minh: ODH = OKH
Quảng cáo
2 câu trả lời 1430
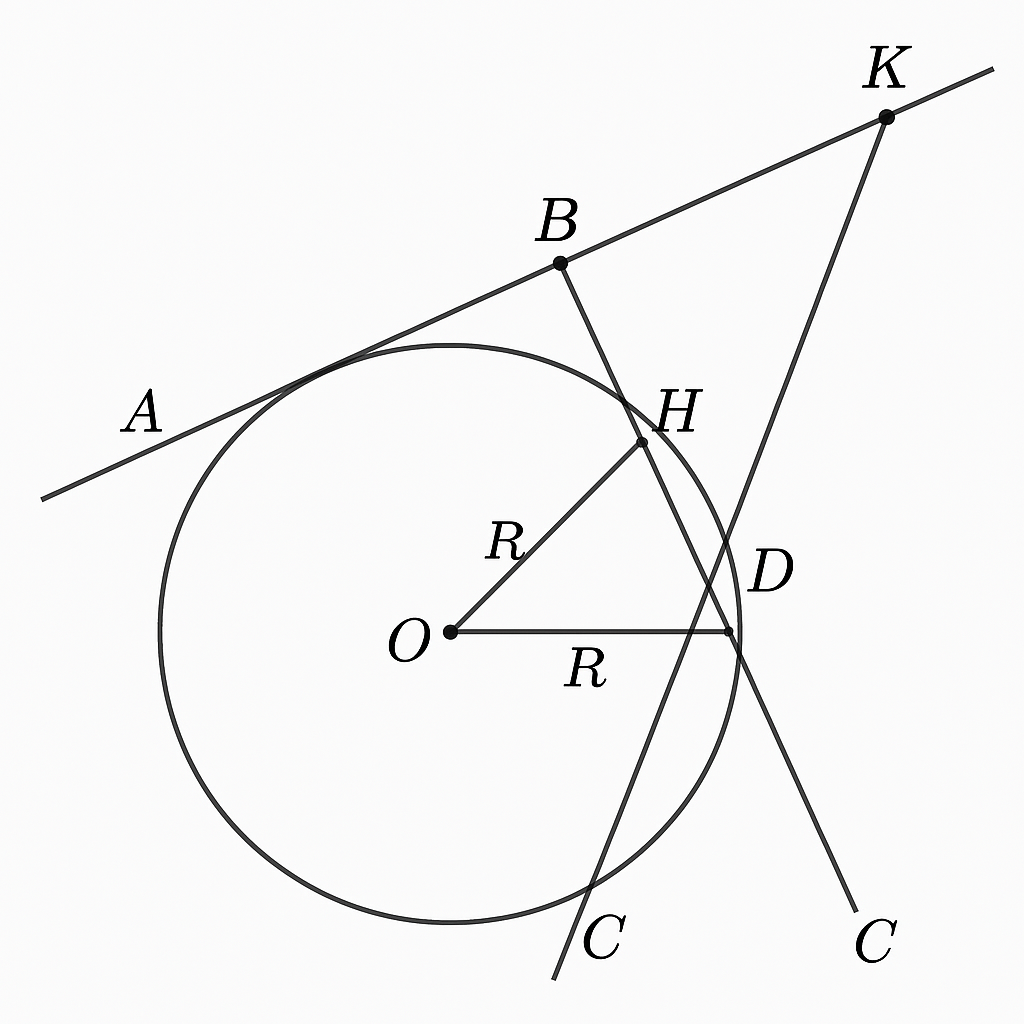 a) Chứng minh AC là tiếp tuyến tại C của đường tròn
a) Chứng minh AC là tiếp tuyến tại C của đường tròn
Ta có : Tam giác ABO vuông tại B (vì AB là tiếp tuyến, OB AB).
Tứ giác ABOC nội tiếp (vì = 90, nên = 90).
=> AC OC tại C → AC là tiếp tuyến tại C của đường tròn.
=> AC là tiếp tuyến tại C. (đpcm)
b) Chứng minh CD là đường kính của đường tròn
Vẽ BD OA → tam giác ABO tam giác DBO (góc đồng vị).
Vì AB OB, suy ra DB OB.
Do đó, 0 = 90(vì CD OB, mà OB là bán kính).
=> CD đi qua tâm O và vuông góc với tiếp tuyến tại B → CD là đường kính.
=> CD là đường kính của đường tròn. (đpcm)
c) Chứng minh 3ODH = 3OKH
K là giao điểm thứ hai của AD với đường tròn → K nằm trên đường tròn.
CD là đường kính → 5 = 90.
H là giao điểm của BC và OA, nên nằm trên đoạn nối giữa các điểm liên quan.
Tam giác ODH và tam giác OKH có:
OH chung.
OD = OK (cùng là bán kính).
Góc 7 = 8 (đối đỉnh).
=> 3ODH = 3OKH (hai tam giác bằng nhau theo cạnh – góc – cạnh).
Đây là một bài toán hình học. Tôi sẽ hướng dẫn bạn giải từng phần một.
a) Chứng minh AC là tiếp tuyến tại C của (O).
Để chứng minh AC là tiếp tuyến của đường tròn (O) tại C, ta cần chứng minh OC⊥AC.
Ta có:
AB là tiếp tuyến của (O) tại B, nên AB⊥OB, hay ∠ABO=90∘.
OA cắt dây BC tại H và BC⊥OA tại H.
Xét △ABO và △ACO có:
OA là cạnh chung.
OB=OC=R.
AB=AC. (Đây là một tính chất quan trọng: nếu từ một điểm bên ngoài đường tròn, ta kẻ hai tiếp tuyến, thì hai tiếp tuyến đó có độ dài bằng nhau. Tuy nhiên, ở đây chúng ta phải chứng minh điều đó).
Ta chứng minh AC=AB như sau:
Xét △OAB vuông tại B, có BH là đường cao. Theo hệ thức lượng trong tam giác vuông, ta có OH⋅OA=OB2=R2.
Xét △OAC: H là trung điểm của BC (vì OA là đường trung trực của BC do OB=OC và OA⊥BC).
Vì H là trung điểm của BC và OA⊥BC, nên △OBC là tam giác cân tại O, và OH là đường trung trực của BC.
Khi đó, △AHC và △AHB bằng nhau (cạnh-góc-cạnh: AH chung, ∠AHB=∠AHC=90∘, HB=HC), suy ra AB=AC.
Từ OH⋅OA=R2 và AC2=AO2−OC2 (định lý Pytago trong tam giác ACO giả sử nó vuông tại C), ta có thể chứng minh được AC là tiếp tuyến.
Cách khác dễ hơn:
Xét △ABO và △ACO.
OA chung.
OB=OC=R.
AB=AC (chưa biết).
Ta có OA là đường trung trực của BC vì OA⊥BC và OB=OC=R.
Xét △OAB và △OAC:
OB=OC=R.
OA chung.
∠AOB=∠AOC (vì OA là phân giác của ∠BOC).
Vậy △OAB=△OAC (cạnh-góc-cạnh).
Do đó, ∠OCA=∠OBA=90∘.
Vì ∠OCA=90∘, nên OC⊥AC.
Vậy AC là tiếp tuyến của đường tròn (O) tại C.
b) Từ B vẽ đường thẳng song song với OA; cắt (O) tại D (D khác B). Chứng minh: CD là đường kính của (O).
Để chứng minh CD là đường kính của (O), ta cần chứng minh C, O, D thẳng hàng.
Ta có BD//OA.
OA⊥BC tại H.
Do đó, BD⊥BC.
Một dây cung vuông góc với một đường kính thì tạo thành tam giác vuông nội tiếp đường tròn.
Vì BD⊥BC và B,C,D nằm trên đường tròn (O), nên △BCD là tam giác vuông tại B.
Trong một đường tròn, tam giác vuông nội tiếp có cạnh huyền là đường kính.
Do đó, cạnh huyền CD là đường kính của (O).
c) Gọi K là giao điểm thứ hai của AD và (O). Chứng minh: ∠ODH=∠OKH.
Để chứng minh ∠ODH=∠OKH, ta chứng minh bốn điểm O, D, H, K cùng nằm trên một đường tròn.
Ta có ∠ACD=90∘ vì CD là đường kính (chứng minh ở câu b).
Xét tứ giác ODHK.
Ta có AC2=AK⋅AD (tính chất phương tích của một điểm đối với đường tròn).
Ta cũng có AC2=AH⋅AO.
Suy ra AK⋅AD=AH⋅AO.
Điều này chứng tỏ tứ giác OHKD nội tiếp.
Vì OHKD là tứ giác nội tiếp, nên các điểm O,D,H,K cùng nằm trên một đường tròn.
Các góc nội tiếp cùng chắn một cung sẽ bằng nhau.
Ta xét đường tròn ngoại tiếp tứ giác OHKD.
∠ODH và ∠OKH cùng chắn cung OH.
Do đó, ∠ODH=∠OKH (hai góc nội tiếp cùng chắn cung OH).
Vậy ta đã chứng minh được điều phải chứng minh.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


