Cho(O;R), đường thẳng không đi qua (O), d cắt (O) tại C, D. Từ điểm M bất kì trên d (C nằm giữa M và D và nằm ngoài (O)) kẻ 2 tiếp tuyến MA, MB với (O). Gọi H là giao điểm của AB và MO , I là trung điểm của CD.
Quảng cáo
3 câu trả lời 280
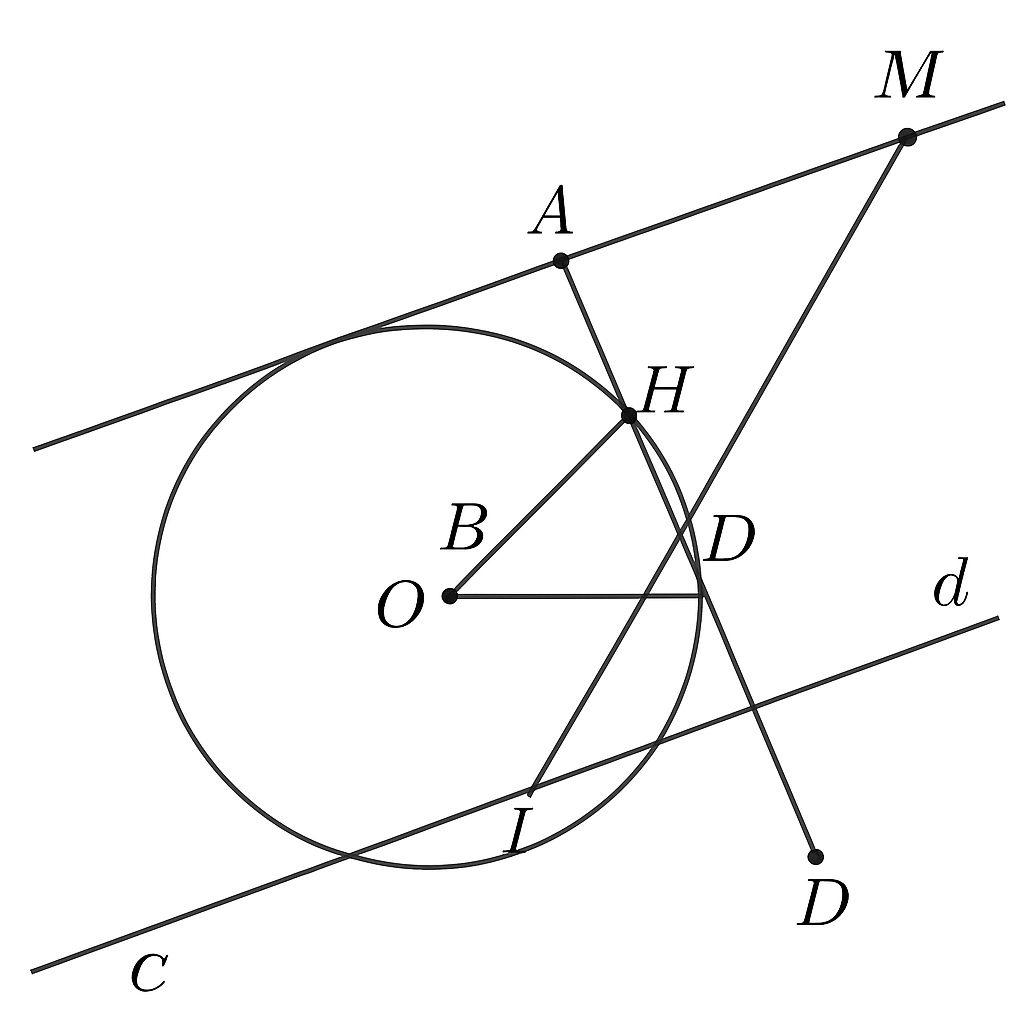
1. Chứng minh tứ giác MAOB nội tiếp
Vì MA, MB là hai tiếp tuyến từ điểm M đến đường tròn tâm O, nên:
MA OA tại A
MB OB tại B
⇒ = = 90
=> Tứ giác MAOB có hai góc vuông ⇒ nội tiếp đường tròn.
=> MAOB là tứ giác nội tiếp (đpcm)
2. Chứng minh OH AB
Gọi H là giao điểm của AB và MO.
Ta có:
MA = MB (hai tiếp tuyến từ một điểm ngoài đường tròn)
OA = OB (hai bán kính) ⇒ Tam giác MAO bằng tam giác MBO (cạnh – góc vuông – cạnh)
⇒ = , nên AB là dây đối xứng qua đường thẳng MO
=> OH là đường trung trực của dây AB ⇒ OH AB (đpcm)
3. Chứng minh OI CD
Gọi I là trung điểm của đoạn CD.
Vì C, D nằm trên đường tròn tâm O, nên:
Đường nối từ tâm O đến trung điểm của dây CD luôn vuông góc với dây đó.
=> OI CD
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


