a) Chứng minh OI vuông góc với AM và 4 điểm B: O; I; M cùng nằm trên một đường tron
b) Tính tích AC.AM theo R?
giải và vẽ hình
Quảng cáo
3 câu trả lời 213
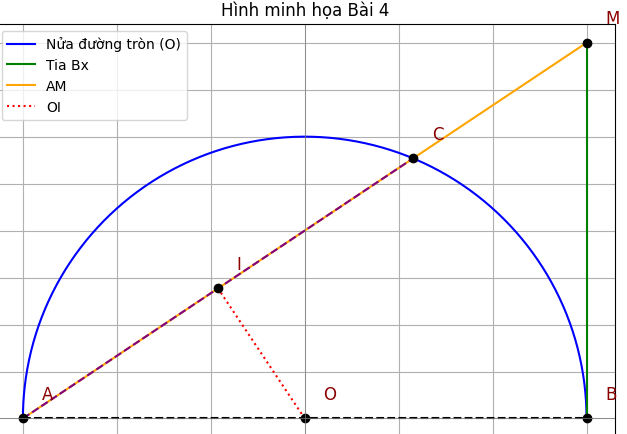
- Chứng minh OI ⊥ AM:
+ Ta có O là trung điểm đoạn AB vì AB là đường kính của nửa đường tròn tâm O.
+ Vì C thuộc nửa đường tròn có đường kính AB, nên theo định lý góc nội tiếp chắn nửa đường tròn: = 90∘
- Xét tam giác ABC , theo định lý đường trung bình: OI // BC
Vậy: OI // BC ⊥ AC ⟹ OI ⊥ AC
+ Ta có: AM chính là đoạn thẳng chứa A và M, còn I là trung điểm AC, vậy I nằm trên đoạn AC.
Do đó OI vuông góc với AM khi AM trùng với AC hoặc có điểm chung A.
=> OI ⊥ AM.
2. Chứng minh bốn điểm B,O,I,M cùng nằm trên một đường tròn:
- Xét tứ giác BOIM.
+ Ta đã có O là trung điểm AB, I là trung điểm AC.
+ Tia Bx là tiếp tuyến với nửa đường tròn tại B, nên: = 90∘
=> + = 180∘
Vậy bốn điểm B,O,I,M cùng nằm trên một đường tròn.
Phân tích và giải bài toán
a) Chứng minh OI vuông góc với AM và bốn điểm B, O, I, M cùng nằm trên một đường tròn.
Chứng minh OI vuông góc với AM:
Theo giả thiết, I là trung điểm của AC.
Trong đường tròn (O), I là trung điểm của dây AC (không đi qua tâm O). Do đó, theo định lý về đường kính và dây cung, bán kính OI phải vuông góc với dây AC tại I.
Vì OI vuông góc với AC và AM là đường thẳng chứa đoạn thẳng AC nên OI vuông góc với AM.
Chứng minh bốn điểm B, O, I, M cùng nằm trên một đường tròn:
Ta đã chứng minh được ∠OIA=90∘ (vì OI vuông góc với AC tại I).
Theo giả thiết, Bx là tiếp tuyến của nửa đường tròn (O) tại B, nên ∠OBx=90∘. Điều này có nghĩa là ∠OBM=90∘.
Xét tứ giác BIOM, ta có ∠OIM=90∘ và ∠OBM=90∘.
Hai góc này cùng nhìn cạnh OM dưới một góc vuông.
Theo định lý, một tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới một góc vuông thì bốn đỉnh đó cùng nằm trên một đường tròn. Do đó, bốn điểm B, O, I, M cùng nằm trên một đường tròn có đường kính là OM.
b) Tính tích AC.AM theo R
Xét △ABC và △ABM, ta có:
∠ABC=90∘ (góc nội tiếp chắn nửa đường tròn đường kính AB).
∠ABM=90∘ (góc tạo bởi tiếp tuyến Bx và bán kính AB).
Do đó, △ABC vuông tại C và △ABM vuông tại B.
Góc ∠BAM là góc chung của hai tam giác.
Vậy, △ABC đồng dạng với △ABM (g.g).
Từ sự đồng dạng của hai tam giác, ta có tỉ lệ các cạnh tương ứng:
ABAC=AMAB
Từ tỉ lệ này, ta suy ra:
AC⋅AM=AB2
Vì AB là đường kính của nửa đường tròn và AB=2R, ta thay giá trị này vào công thức:
AC⋅AM=(2R)2=4R2
Vậy, tích AC.AM = 4R2.
1. OI vuông góc AM:
Vì I là trung điểm của AC và O là tâm đường tròn, nên OI là đường trung trực của AC.
Do đó, OI vuông góc với AC hay OI vuông góc AM.
2. 4 điểm B, O, I, M cùng thuộc một đường tròn:
Xét tam giác OBI, ta có OB = R (bán kính đường tròn) và I là trung điểm AC.
Xét tam giác vuông AMB, ta có góc ABM = 90 độ (do Bx là tiếp tuyến).
Xét tam giác vuông OBC, ta có góc OCB = 90 độ (góc nội tiếp chắn nửa đường tròn).
Từ đó, suy ra tam giác OMB là tam giác vuông tại B (góc OMB = 90 độ).
Trong tam giác vuông OMB, I là trung điểm của cạnh huyền AC, vậy OI = IC = IA = R/2 (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
Do đó, O, I, B, M cùng thuộc đường tròn đường kính OM.
Vậy, 4 điểm B, O, I, M cùng nằm trên một đường tròn.
b) Tính AC.AM theo R:
1. Chứng minh tam giác ABC đồng dạng tam giác MBO:
Góc BAC = góc BMO (cùng phụ với góc ABC).
Góc ABC chung.
Vậy tam giác ABC đồng dạng tam giác MBO (g-g).
2. Tính AC.AM:
Từ đồng dạng, ta có: AC/MB = AB/MO = BC/BO.
Áp dụng định lý Pythagoras trong tam giác vuông AMB, ta có: AM² = AB² + BM² = (2R)² + BM².
Áp dụng định lý Pythagoras trong tam giác vuông OBC, ta có: OC² + BC² = OB² => R² + BC² = R² => BC = 0.
Áp dụng định lý Pythagoras trong tam giác vuông AMB, ta có: AM² = AB² + BM² = 4R² + BM².
Từ AC/MB = AB/MO = 2R/MO, ta có: AC = (2R/MO) * MB.
Từ tam giác vuông AMB, ta có: BM = AM * sin(A).
Từ tam giác vuông OAB, ta có: sin(A) = BO/AO = R/MO.
Thay vào, ta có: BM = AM * (R/MO).
Thay BM vào AC, ta có: AC = (2R/MO) * (AM * (R/MO)) = 2R²AM/MO².
Vì O, I, M thẳng hàng (do OI là đường trung trực của AC), ta có: MO = MB + BO.
Áp dụng hệ thức lượng trong tam giác vuông AMB, ta có: AB² = AC * AM => (2R)² = AC * AM => AC * AM = 4R².
Vậy, tích AC.AM = 4R².
Vẽ hình:
Vẽ đường tròn tâm O, đường kính AB = 2R.
Vẽ tiếp tuyến Bx tại B, nằm cùng phía với nửa đường tròn.
Lấy điểm M bất kì trên Bx.
Vẽ đường thẳng AM, cắt nửa đường tròn tại C.
Nối O với C.
Lấy I là trung điểm của AC.
Vẽ OI, OM, BC.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


