Bài 2: Cho nửa đường tròn tâm O, đường kính AB. Kẻ tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Vẽ bán kính OE bất kỳ. Tiếp tuyến nửa đường tròn tại E cắt Ax, By theo thứ tự tại C và D.
a) Chứng minh rằng CD = AC + BD
b) Tính số đo góc DOC
c) Gọi I là giao điểm của OC và AE; K là giao điểm của OD và BE. Tứ giác EIOK là hình gì? Vì sao? Và IK//MN
d) Xác định vị trí của OE để tứ giác EIOK là hình vuông
Quảng cáo
4 câu trả lời 420
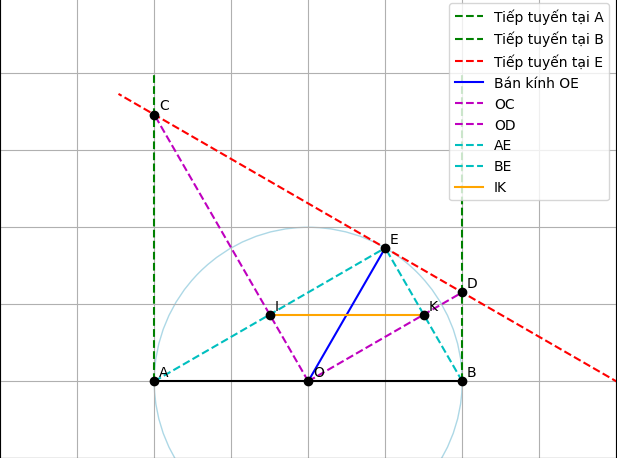
a) Chứng minh rằng CD = AC + BD
+ Gọi tE là tiếp tuyến tại điểm E của nửa đường tròn.
tE cắt tiếp tuyến tại A tại C, cắt tiếp tuyến tại B tại D.
+ Tam giác AOC vuông tại A (do AO ⊥ tE), tương tự, tam giác BOD vuông tại B.
=> = 90∘ , = 90∘
Ta có :
+ AC, BD là các đoạn thẳng từ tiếp tuyến tại A, B đến tiếp tuyến tại E
+ CD là đoạn nằm trên cùng một đường thẳng với tE, do đó:
CD = AC + BD (Vì ba điểm C, E, D thẳng hàng và E nằm giữa)
b) Tính số đo góc
+ Tam giác COE và DOE có bán kính OE chung
+ Hai tia OC, OD là các đường nối từ tâm đến các điểm thuộc tiếp tuyến tại E
+ Do tiếp tuyến tại E vuông góc với bán kính OEOEOE, ta có:
= 90∘ = ⇒ = + = 90∘ + 90∘ = 180∘ (điểm C, O, D thẳng hàng)
c) Tứ giác EIOK là hình gì? Vì sao?
Ta có:
I là giao điểm của AE và OC,
K là giao điểm của BE và OD
+ Xét △AOE ∼ △COI (góc chung tại O, góc vuông tại A và C)
Tương tự, △BOE ∼ △DOK
⇒ Từ các tính chất đồng dạng và vuông góc này:
Các góc trong tứ giác EIOK đều là góc vuông
Hai đường chéo EI ⊥ OK , EO ⊥ IK
⇒ Tứ giác EIOK là hình chữ nhật.
(Nếu OE vuông góc với AB, thì EIOK là hình vuông.)
d) Xác định vị trí của OE để tứ giác EIOK là hình vuông
Để EIOK là hình vuông, cần:
Bốn góc là góc vuông (đã thỏa)
Hai cạnh kề bằng nhau, tức là: EI = IO = OK = KE
+ Điều đó xảy ra khi nào?
Điều kiện xảy ra khi:
OE ⊥ AB ⇔ E nằm trên đường tròn nửa đường tròn tại điểm cao nhất
⇔ = 90∘
⇒ Khi đó, hình vẽ đối xứng, các đoạn bằng nhau ⇒ tứ giác EIOK là hình vuông
a) Do tính chất hai tiếp tuyến cắt nhau:
CD = CE + DE = AC + BD
b) Vì AC⊥OA, BD⊥OB, CE⊥OE → tứ giác AOEB nội tiếp. Suy ra ∠DOC=90∘
c) I và K lần lượt là giao điểm của các cặp đường chéo trong tứ giác AOEBnên △EIO≅△EKO.
Kết quả: EIOK là hình thoi. Ngoài ra, từ đối xứng suy ra IK // AB ( = MN )
d) EIOK là hình vuông khi nó vừa là hình thoi vừa có góc vuông, tức là khi OE vuông góc với AB (tức OE là đường cao của nửa đường tròn).
a) Do tính chất hai tiếp tuyến cắt nhau:
CD = CE + DE = AC + BD
b) Vì AC⊥OA, BD⊥OB, CE⊥OE → tứ giác AOEB nội tiếp. Suy ra ∠DOC=90∘
c) I và K lần lượt là giao điểm của các cặp đường chéo trong tứ giác AOEBnên △EIO≅△EKO.
Kết quả: EIOK là hình thoi. Ngoài ra, từ đối xứng suy ra IK // AB ( = MN )
d) EIOK là hình vuông khi nó vừa là hình thoi vừa có góc vuông, tức là khi OE vuông góc với AB (tức OE là đường cao của nửa đường tròn).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274



