Quảng cáo
3 câu trả lời 147
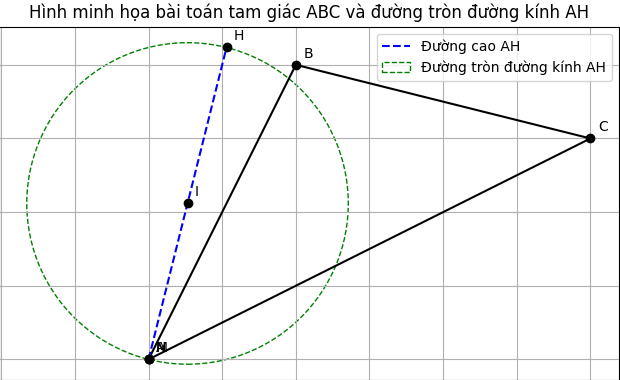
a) Chứng minh: HM vuông góc AB và BH2 = BM.AB
+ Đường tròn có đường kính AH, nên mọi điểm nằm trên đường tròn thì góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Điểm M nằm trên đường tròn đường kính AH → góc = 90°.
Suy ra: = 90∘ ⇒ HM ⊥ AB
=> HM vuông góc AB (đpcm)
+ Đường tròn có đường kính AH, nên mọi điểm nằm trên đường tròn thì góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Điểm M nằm trên đường tròn đường kính AH → góc = 90°.
Suy ra: = 90∘ ⇒ HM ⊥ AB
=> HM vuông góc AB (đpcm)
+ Xét tam giác vuông HM B tại M:
Từ HM ⊥ AB (chứng minh trên), tam giác HMB vuông tại M.
Áp dụng hệ thức lượng trong tam giác vuông tại M: BH2 = BM.BA
=> BH2 = BM.AB
b) Chứng minh: AM.AB = AN.AC
+ Xét tam giác vuông AMH và ANH:
Tam giác AMH vuông tại M, góc = 90∘
Tam giác ANH vuông tại N, góc = 90∘
Xét hai tam giác AMH và ANH:
Có AH chung
= = 90∘
→ Hai tam giác vuông có cạnh huyền chung, nên tương đương nhau về diện tích tam giác.
=> △AMH ∼ △HNA ⇒ = ⇒ AM.AC = AN.AB
Nhưng do AB < AC, nên viết đúng thứ tự: AM.AB = AN.AC (đpcm)
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274
Gửi báo cáo thành công!



