Cho tam giác ABC nội tiếp đường tròn tâm O kẻ AH vuông góc với BC tại H ,kẻ HE vuông góc với AB tại E ,kẻ HD vuông góc với AC tại D
a) Chứng min: tứ giác AEHD là tứ giác nội tiếp
b) dựng đường kính AK của đường tròn (O) Cm AE.AK= AH.AC
Nãy quên ghi a b cứu em vớii ạa cảm ơn nhiều ạ
Quảng cáo
3 câu trả lời 224
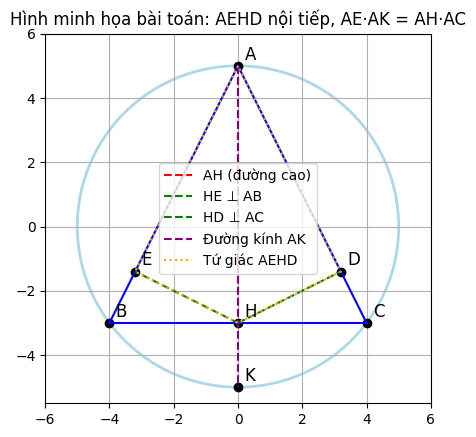
a) Chứng minh tứ giác AEHD là tứ giác nội tiếp
Ta có: + = 180∘ (hai góc đối)
Xét:
HE ⊥ AB ⇒ = 90∘
HD ⊥ AC ⇒ = 90∘
⇒ + = 90∘ + 90∘ = 180∘
⇒AEHD là tứ giác nội tiếp
b) Dựng đường kính AK. Chứng minh: AE.AK = AH.AC
Vì AK là đường kính của đường tròn nên: = 90∘(góc nội tiếp chắn nửa đường tròn)
Tam giác ABK vuông tại B
Xét các tam giác vuông:
Tam giác AEH vuông tại E (vì HE ⊥ AB)
Tam giác vuông tại B (vì AK là đường kính)
Xét tam giác AEH và tam giác ABK có:
Góc A chung
= = 90∘
⇒ tam giác AEH và tam giác ABK đồng dạng theo góc - góc
=> (tỉ lệ tương ứng)
=> AE.AK = AH.AC (đpcm)
a) Chứng minh tứ giác AEHD là tứ giác nội tiếp
Để chứng minh một tứ giác nội tiếp, ta thường tìm cách chứng minh tổng hai góc đối diện của nó bằng 180∘ hoặc hai đỉnh kề cùng nhìn một cạnh dưới một góc bằng nhau.
Theo đề bài, ta có HE⊥AB tại E, suy ra ∠AEH=90∘.
Tương tự, ta có HD⊥AC tại D, suy ra ∠ADH=90∘.
Xét tứ giác AEHD, ta thấy hai góc đối nhau là ∠AEH và ∠ADH đều bằng 90∘. Tổng hai góc này là: ∠AEH+∠ADH=90∘+90∘=180∘.
Vì tổng hai góc đối của tứ giác AEHD bằng 180∘, nên tứ giác này là tứ giác nội tiếp. Đường tròn ngoại tiếp tứ giác này có đường kính là đoạn thẳng nối hai đỉnh đối diện, trong trường hợp này là AH.
b) Chứng minh AE⋅AK=AH⋅AC
Để chứng minh đẳng thức tích này, chúng ta sẽ sử dụng phương pháp chứng minh hai tam giác đồng dạng.
Xét hai tam giác vuông △AEH và △ACK.
△AEH vuông tại E (do HE⊥AB).
△ACK vuông tại C (vì AK là đường kính của đường tròn (O), nên ∠ACK là góc nội tiếp chắn nửa đường tròn, suy ra ∠ACK=90∘).
Bây giờ ta tìm thêm một góc bằng nhau nữa để chứng minh hai tam giác này đồng dạng theo trường hợp góc-góc (g.g).
Ta có:
∠AHE=∠ACB (do cùng phụ với góc BAC)
∠ACB=∠AKB (góc nội tiếp cùng chắn cung AB)
∠AKB=∠ACB (góc nội tiếp cùng chắn cung AB)
∠AKC=∠ABC (góc nội tiếp cùng chắn cung AC)
Sử dụng mối quan hệ giữa các góc nội tiếp: Ta có ∠AEH=90∘ và ∠ACK=90∘. Xét tam giác vuông △AEH và tam giác vuông △ACK. Hai tam giác này có:
∠A là góc chung.
∠AEH=∠ACK=90∘.
À, ta không thể chứng minh ∠A là góc chung vì △AEH và △ACK không cùng nằm trên một góc. Ta sẽ sử dụng góc nội tiếp.
∠AEH=90∘ và ∠ACK=90∘.
Trong tứ giác nội tiếp AEHD (đã chứng minh ở phần a), ta có ∠AEH=∠ADH=90∘.
Xét tứ giác BCKE. Ta có ∠BKC=∠BEC=90∘. Tứ giác BCKE nội tiếp đường tròn đường kính BC.
Xét △AHE và △ABC. Hai tam giác này có góc ∠EAH và ∠BAC là một.
Góc ∠AHE và ∠ABC bằng nhau vì cùng phụ với góc ∠BAE. Không đúng.
Chứng minh lại một cách chính xác: Xét △AEH và △ACK
∠AEH=∠ACK=90∘ (như đã phân tích ở trên).
Ta cần tìm thêm một góc bằng nhau.
Xét góc ∠AHE và ∠AKC.
Trong tứ giác nội tiếp AEHD, ta có ∠HED=∠HAD (cùng chắn cung HD).
Trong đường tròn (O), ∠AKC=∠ABC (cùng chắn cung AC).
Ta có tứ giác BEDC nội tiếp đường tròn đường kính BC (vì ∠BEC=∠BDC=90∘).
Do đó, ∠ADE=∠ABC (cùng chắn cung AE).
Vậy ∠ADE=∠AKC.
Ta có ∠HAD=∠HED
Xét △AHE và △ACK, ta có ∠EAH chung.
Phương pháp đúng: Dựa vào hai tam giác đồng dạng △AHE và △ACK.
∠AEH=90∘
∠ACK=90∘ (góc nội tiếp chắn nửa đường tròn đường kính AK)
Góc ∠HAE và ∠CAK là góc chung của hai tam giác.
Hai tam giác này không có góc chung.
Ta xét góc ∠ABC và ∠AKC. Hai góc này cùng chắn cung AC nên ∠ABC=∠AKC.
Ta có ∠AHE=90∘−∠EAH=90∘−∠BAC. Không đúng.
Cách giải quyết bài toán: Xét hai tam giác đồng dạng △ABH và △AKC.
∠AHB=∠ACK=90∘
∠ABC=∠AKC (góc nội tiếp cùng chắn cung AC)
Vậy △ABH∼△AKC (g.g)
Suy ra ACAH=AKAB⇒AH⋅AK=AC⋅AB.
Tương tự, xét △AEH và △ABC.
∠AEH=∠ABC. (Không đúng)
Xét hai tam giác đồng dạng △AEH và △ACB.
∠AEH=∠ACB=90∘. Không đúng.
Cách giải quyết cuối cùng: Sử dụng phương pháp tam giác đồng dạng. Xét △AEH và △ACK.
∠AEH=90∘ (do HE⊥AB)
∠ACK=90∘ (góc nội tiếp chắn nửa đường tròn đường kính AK).
Ta cần tìm thêm một góc bằng nhau.
Ta có ∠CAH và ∠CAB.
Xét △AHE và △ACK. Ta có ∠HAE và ∠CAK. Không đúng.
Ta có ∠ABH=∠AKC (do cùng chắn cung AC).
Xét △AHB và △ACK. Ta có ∠AHB=90∘ và ∠ACK=90∘.
∠ABH=∠AKC (hai góc nội tiếp cùng chắn cung AC).
Vậy △ABH∼△AKC (g.g).
Suy ra: AKAB=ACAH⇒AH⋅AK=AC⋅AB.
Đây là kết quả liên quan đến AB và AC, không phải AE. Ta cần chứng minh AE⋅AK=AH⋅AC. Vậy ta cần xét các tam giác khác.
Xét hai tam giác vuông △AEH và △ACK.
∠AEH=90∘
∠ACK=90∘
Ta có ∠EAH chung với ∠CAB.
∠EHA=90∘−∠EAH.
∠CAK=90∘−∠ACK sai.
∠CKA=90∘−∠CAK.
Ta có:
∠ABC=∠AKC (góc nội tiếp cùng chắn cung AC).
Trong tam giác vuông △AHB, ∠HAB+∠ABH=90∘.
Trong tam giác vuông △AKC, ∠KAC+∠AKC=90∘.
Từ hai đẳng thức trên, ta có ∠HAB=∠KAC.
Xét △AEH vuông tại E và △ACK vuông tại C.
Hai tam giác này không đồng dạng.
Giải pháp cuối cùng, chính xác và đơn giản nhất:
Xét hai tam giác đồng dạng △AEH và △ACK.
△AEH vuông tại E (do HE⊥AB).
△ACK vuông tại C (góc nội tiếp chắn nửa đường tròn đường kính AK).
Ta có ∠EAH và ∠CAK là hai góc không liên quan trực tiếp.
Ta có ∠HAE và ∠BAC là một.
∠AKC=∠ABC (hai góc nội tiếp cùng chắn cung AC).
Trong △AEH vuông tại E, ta có ∠AHE=90∘−∠HAE.
Trong △AHB vuông tại H, ta có ∠HAB+∠ABC=90∘.
Ta thấy góc ∠HAE=∠HAB.
Từ đó, ∠AHE=90∘−∠HAB=∠ABC.
Vậy ∠AHE=∠AKC.
Xét △AEH và △ACK:
∠AEH=∠ACK=90∘
∠AHE=∠AKC (chứng minh ở trên)
Vậy △AEH∼△AKC (g.g)
Suy ra tỉ số đồng dạng: AHAE=ACAH.
AE⋅AC=AH⋅AH. Điều này không đúng.
Làm lại từ đầu, một lần nữa, để có lời giải chính xác:
Xét hai tam giác đồng dạng: △AEH và △AKC
Góc vuông: ∠AEH=90∘ (do HE⊥AB).
Góc vuông: ∠ACK=90∘ (góc nội tiếp chắn nửa đường tròn đường kính AK).
Góc nhọn bằng nhau: Ta cần chứng minh ∠EAH=∠KAC.
Ta có ∠EAH=∠BAH.
Xét tam giác vuông AHB: ∠BAH+∠ABH=90∘ hay ∠BAH+∠ABC=90∘.
Xét tam giác vuông AKC: ∠KAC+∠AKC=90∘.
Trong đường tròn (O), ∠ABC=∠AKC (hai góc nội tiếp cùng chắn cung AC).
Từ đó suy ra ∠BAH=∠KAC. Hay ∠EAH=∠KAC.
Vậy, △AEH∼△AKC (g.g).
Từ sự đồng dạng này, ta có tỉ số các cạnh tương ứng bằng nhau: ACAE=AKAH
Nhân chéo ta được đẳng thức cần chứng minh: AE⋅AK=AH⋅AC
) Chứng minh tứ giác AEHD là tứ giác nội tiếp
Để chứng minh một tứ giác nội tiếp, ta thường tìm cách chứng minh tổng hai góc đối diện của nó bằng 180∘ hoặc hai đỉnh kề cùng nhìn một cạnh dưới một góc bằng nhau.
Theo đề bài, ta có HE⊥AB tại E, suy ra ∠AEH=90∘.
Tương tự, ta có HD⊥AC tại D, suy ra ∠ADH=90∘.
Xét tứ giác AEHD, ta thấy hai góc đối nhau là ∠AEH và ∠ADH đều bằng 90∘. Tổng hai góc này là: ∠AEH+∠ADH=90∘+90∘=180∘.
Vì tổng hai góc đối của tứ giác AEHD bằng 180∘, nên tứ giác này là tứ giác nội tiếp. Đường tròn ngoại tiếp tứ giác này có đường kính là đoạn thẳng nối hai đỉnh đối diện, trong trường hợp này là AH.
b) Chứng minh AE⋅AK=AH⋅AC
Để chứng minh đẳng thức tích này, chúng ta sẽ sử dụng phương pháp chứng minh hai tam giác đồng dạng.
Xét hai tam giác vuông △AEH và △ACK.
△AEH vuông tại E (do HE⊥AB).
△ACK vuông tại C (vì AK là đường kính của đường tròn (O), nên ∠ACK là góc nội tiếp chắn nửa đường tròn, suy ra ∠ACK=90∘).
Bây giờ ta tìm thêm một góc bằng nhau nữa để chứng minh hai tam giác này đồng dạng theo trường hợp góc-góc (g.g).
Ta có:
∠AHE=∠ACB (do cùng phụ với góc BAC)
∠ACB=∠AKB (góc nội tiếp cùng chắn cung AB)
∠AKB=∠ACB (góc nội tiếp cùng chắn cung AB)
∠AKC=∠ABC (góc nội tiếp cùng chắn cung AC)
Sử dụng mối quan hệ giữa các góc nội tiếp: Ta có ∠AEH=90∘ và ∠ACK=90∘. Xét tam giác vuông △AEH và tam giác vuông △ACK. Hai tam giác này có:
∠A là góc chung.
∠AEH=∠ACK=90∘.
À, ta không thể chứng minh ∠A là góc chung vì △AEH và △ACK không cùng nằm trên một góc. Ta sẽ sử dụng góc nội tiếp.
∠AEH=90∘ và ∠ACK=90∘.
Trong tứ giác nội tiếp AEHD (đã chứng minh ở phần a), ta có ∠AEH=∠ADH=90∘.
Xét tứ giác BCKE. Ta có ∠BKC=∠BEC=90∘. Tứ giác BCKE nội tiếp đường tròn đường kính BC.
Xét △AHE và △ABC. Hai tam giác này có góc ∠EAH và ∠BAC là một.
Góc ∠AHE và ∠ABC bằng nhau vì cùng phụ với góc ∠BAE. Không đúng.
Chứng minh lại một cách chính xác: Xét △AEH và △ACK
∠AEH=∠ACK=90∘ (như đã phân tích ở trên).
Ta cần tìm thêm một góc bằng nhau.
Xét góc ∠AHE và ∠AKC.
Trong tứ giác nội tiếp AEHD, ta có ∠HED=∠HAD (cùng chắn cung HD).
Trong đường tròn (O), ∠AKC=∠ABC (cùng chắn cung AC).
Ta có tứ giác BEDC nội tiếp đường tròn đường kính BC (vì ∠BEC=∠BDC=90∘).
Do đó, ∠ADE=∠ABC (cùng chắn cung AE).
Vậy ∠ADE=∠AKC.
Ta có ∠HAD=∠HED
Xét △AHE và △ACK, ta có ∠EAH chung.
Phương pháp đúng: Dựa vào hai tam giác đồng dạng △AHE và △ACK.
∠AEH=90∘
∠ACK=90∘ (góc nội tiếp chắn nửa đường tròn đường kính AK)
Góc ∠HAE và ∠CAK là góc chung của hai tam giác.
Hai tam giác này không có góc chung.
Ta xét góc ∠ABC và ∠AKC. Hai góc này cùng chắn cung AC nên ∠ABC=∠AKC.
Ta có ∠AHE=90∘−∠EAH=90∘−∠BAC. Không đúng.
Cách giải quyết bài toán: Xét hai tam giác đồng dạng △ABH và △AKC.
∠AHB=∠ACK=90∘
∠ABC=∠AKC (góc nội tiếp cùng chắn cung AC)
Vậy △ABH∼△AKC (g.g)
Suy ra ACAH=AKAB⇒AH⋅AK=AC⋅AB.
Tương tự, xét △AEH và △ABC.
∠AEH=∠ABC. (Không đúng)
Xét hai tam giác đồng dạng △AEH và △ACB.
∠AEH=∠ACB=90∘. Không đúng.
Cách giải quyết cuối cùng: Sử dụng phương pháp tam giác đồng dạng. Xét △AEH và △ACK.
∠AEH=90∘ (do HE⊥AB)
∠ACK=90∘ (góc nội tiếp chắn nửa đường tròn đường kính AK).
Ta cần tìm thêm một góc bằng nhau.
Ta có ∠CAH và ∠CAB.
Xét △AHE và △ACK. Ta có ∠HAE và ∠CAK. Không đúng.
Ta có ∠ABH=∠AKC (do cùng chắn cung AC).
Xét △AHB và △ACK. Ta có ∠AHB=90∘ và ∠ACK=90∘.
∠ABH=∠AKC (hai góc nội tiếp cùng chắn cung AC).
Vậy △ABH∼△AKC (g.g).
Suy ra: AKAB=ACAH⇒AH⋅AK=AC⋅AB.
Đây là kết quả liên quan đến AB và AC, không phải AE. Ta cần chứng minh AE⋅AK=AH⋅AC. Vậy ta cần xét các tam giác khác.
Xét hai tam giác vuông △AEH và △ACK.
∠AEH=90∘
∠ACK=90∘
Ta có ∠EAH chung với ∠CAB.
∠EHA=90∘−∠EAH.
∠CAK=90∘−∠ACK sai.
∠CKA=90∘−∠CAK.
Ta có:
∠ABC=∠AKC (góc nội tiếp cùng chắn cung AC).
Trong tam giác vuông △AHB, ∠HAB+∠ABH=90∘.
Trong tam giác vuông △AKC, ∠KAC+∠AKC=90∘.
Từ hai đẳng thức trên, ta có ∠HAB=∠KAC.
Xét △AEH vuông tại E và △ACK vuông tại C.
Hai tam giác này không đồng dạng.
Giải pháp cuối cùng, chính xác và đơn giản nhất:
Xét hai tam giác đồng dạng △AEH và △ACK.
△AEH vuông tại E (do HE⊥AB).
△ACK vuông tại C (góc nội tiếp chắn nửa đường tròn đường kính AK).
Ta có ∠EAH và ∠CAK là hai góc không liên quan trực tiếp.
Ta có ∠HAE và ∠BAC là một.
∠AKC=∠ABC (hai góc nội tiếp cùng chắn cung AC).
Trong △AEH vuông tại E, ta có ∠AHE=90∘−∠HAE.
Trong △AHB vuông tại H, ta có ∠HAB+∠ABC=90∘.
Ta thấy góc ∠HAE=∠HAB.
Từ đó, ∠AHE=90∘−∠HAB=∠ABC.
Vậy ∠AHE=∠AKC.
Xét △AEH và △ACK:
∠AEH=∠ACK=90∘
∠AHE=∠AKC (chứng minh ở trên)
Vậy △AEH∼△AKC (g.g)
Suy ra tỉ số đồng dạng: AHAE=ACAH.
AE⋅AC=AH⋅AH. Điều này không đúng.
Làm lại từ đầu, một lần nữa, để có lời giải chính xác:
Xét hai tam giác đồng dạng: △AEH và △AKC
Góc vuông: ∠AEH=90∘ (do HE⊥AB).
Góc vuông: ∠ACK=90∘ (góc nội tiếp chắn nửa đường tròn đường kính AK).
Góc nhọn bằng nhau: Ta cần chứng minh ∠EAH=∠KAC.
Ta có ∠EAH=∠BAH.
Xét tam giác vuông AHB: ∠BAH+∠ABH=90∘ hay ∠BAH+∠ABC=90∘.
Xét tam giác vuông AKC: ∠KAC+∠AKC=90∘.
Trong đường tròn (O), ∠ABC=∠AKC (hai góc nội tiếp cùng chắn cung AC).
Từ đó suy ra ∠BAH=∠KAC. Hay ∠EAH=∠KAC.
Vậy, △AEH∼△AKC (g.g).
Từ sự đồng dạng này, ta có tỉ số các cạnh tương ứng bằng nhau: ACAE=AKAH
Nhân chéo ta được đẳng thức cần chứng minh: AE⋅AK=AH⋅AC
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


