kiet46224@gmail.com
Hỏi từ APP VIETJACK
Cho tam giác ABC có đường cao BD và CE cắt nhau tại H. Chứng minh
a)Bốn điểm D,E,B,C cùng thuộc một đường tròn
b)Bốn điểm A,E,H,D cùng thuộc một đường tròn
a)Bốn điểm D,E,B,C cùng thuộc một đường tròn
b)Bốn điểm A,E,H,D cùng thuộc một đường tròn
Quảng cáo
3 câu trả lời 677
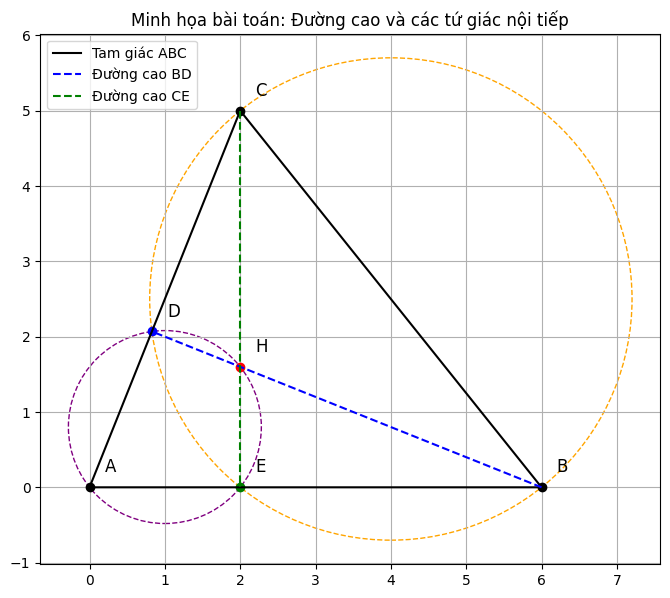
a) Chứng minh bốn điểm D, E, B, C cùng thuộc một đường tròn.
Xét tam giác ABC. Ta có :
Xét tam giác ABC. Ta có :
BD là đường cao của tam giác ABC, nên BD ⊥ AC => = 90∘
CE là đường cao của tam giác ABC, nên CE ⊥ AB => = 90∘
Xét hai góc = = 90∘ và cùng nhìn cạnh BC
Xét hai góc = = 90∘ và cùng nhìn cạnh BC
=> D và E cùng nhìn đoạn thẳng BC dưới hai góc bằng nhau và cùng nằm về một phía so với đường thẳng BC
=> D và E nằm trên đường tròn đường kính BC
=> bốn điểm D, E, B, C cùng thuộc một đường tròn.
b) Chứng minh bốn điểm A, E, H, D cùng thuộc một đường tròn.
Ta có :
Ta có :
BD là đường cao của tam giác ABC, nên BD ⊥ AC => = 90∘
CE là đường cao của tam giác ABC, nên CE ⊥ AB => = 90∘
Xét hai góc = = 90∘ và cùng nhìn cạnh AE dưới góc vuông.
Xét hai góc = = 90∘ và cùng nhìn cạnh AE dưới góc vuông.
Xét hai góc và .
Vì BD là đường cao nên = 90∘
Do H nằm trên BD nên = 90∘
Vì CE là đường cao nên = 90∘
Do H nằm trên CE nên = 90∘.
Xét tứ giác AEHD. Ta có :
Xét tứ giác AEHD. Ta có :
= 90∘ và = 90∘.
Hai góc này cùng nhìn cạnh AH và cùng nằm về một phía so với đường thẳng AH
=> bốn điểm A, E, H, D cùng thuộc một đường tròn.
4 tháng trước
) Chứng minh Bốn điểm D, E, B, C cùng thuộc một đường tròn:
Vì BD và CE là đường cao của tam giác ABC, nên góc BDC và góc BEC đều là góc vuông (90 độ).
Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Do đó, góc BDC và góc BEC cùng chắn cung BC, và chúng bằng nhau (cùng bằng 90 độ).
Vậy, bốn điểm B, D, E, C cùng thuộc một đường tròn (đường tròn đường kính BC).
b) Chứng minh Bốn điểm A, E, H, D cùng thuộc một đường tròn:
Trong tam giác ABC, ta có BD và CE là hai đường cao, giao nhau tại H.
Vì BD và CE là đường cao, nên góc ADB và góc AEC đều là góc vuông (90 độ).
Trong tứ giác AEDH, tổng hai góc đối diện ADB và AEC bằng 180 độ (90 + 90 = 180).
Do đó, tứ giác AEDH là tứ giác nội tiếp (tổng hai góc đối diện bằng 180 độ), suy ra bốn điểm A, E, H, D cùng thuộc một đường tròn.
Vì BD và CE là đường cao của tam giác ABC, nên góc BDC và góc BEC đều là góc vuông (90 độ).
Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Do đó, góc BDC và góc BEC cùng chắn cung BC, và chúng bằng nhau (cùng bằng 90 độ).
Vậy, bốn điểm B, D, E, C cùng thuộc một đường tròn (đường tròn đường kính BC).
b) Chứng minh Bốn điểm A, E, H, D cùng thuộc một đường tròn:
Trong tam giác ABC, ta có BD và CE là hai đường cao, giao nhau tại H.
Vì BD và CE là đường cao, nên góc ADB và góc AEC đều là góc vuông (90 độ).
Trong tứ giác AEDH, tổng hai góc đối diện ADB và AEC bằng 180 độ (90 + 90 = 180).
Do đó, tứ giác AEDH là tứ giác nội tiếp (tổng hai góc đối diện bằng 180 độ), suy ra bốn điểm A, E, H, D cùng thuộc một đường tròn.
4 tháng trước
Để chứng minh các điểm thuộc một đường tròn trong tam giác ABC với các đường cao BD và CE cắt nhau tại H, ta sẽ thực hiện theo các bước sau:
Chứng minh a) Bốn điểm D, E, B, C cùng thuộc một đường tròn-
Xác định các điểm:
- D là chân đường cao từ B xuống cạnh AC.
- E là chân đường cao từ C xuống cạnh AB.
- B và C là các đỉnh của tam giác ABC.
-
Sử dụng tính chất của các đường cao:
- Trong tam giác, các đường cao BD và CE cắt nhau tại H, tạo thành các góc vuông tại D và E.
- Do đó, góc BDC = 90° và góc CED = 90°.
-
Chứng minh góc:
- Ta có góc BDC + góc CED = 90° + 90° = 180°.
- Theo định lý về đường tròn, nếu hai góc ở hai điểm trên một đường tròn có tổng bằng 180°, thì bốn điểm đó nằm trên một đường tròn.
-
Kết luận:
- Do đó, bốn điểm D, E, B, C cùng thuộc một đường tròn.
-
Xác định các điểm:
- A là đỉnh của tam giác ABC.
- E là chân đường cao từ C xuống AB.
- H là giao điểm của hai đường cao BD và CE.
- D là chân đường cao từ B xuống AC.
-
Sử dụng tính chất của các đường cao:
- Tương tự như trên, góc AHE = 90° (vì H là giao điểm của hai đường cao).
- Góc AHD = 90° (vì D là chân đường cao từ B).
-
Chứng minh góc:
- Ta có góc AHE + góc AHD = 90° + 90° = 180°.
- Theo định lý về đường tròn, nếu hai góc ở hai điểm trên một đường tròn có tổng bằng 180°, thì bốn điểm đó nằm trên một đường tròn.
-
Kết luận:
- Do đó, bốn điểm A, E, H, D cùng thuộc một đường tròn.
- Bằng cách sử dụng tính chất của các đường cao và các góc vuông, ta đã chứng minh được rằng:
- Bốn điểm D, E, B, C cùng thuộc một đường tròn.
- Bốn điểm A, E, H, D cùng thuộc một đường tròn.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274
Gửi báo cáo thành công!


