thu thom nguyen
Hỏi từ APP VIETJACK
Cho tứ giác ABCD có góc CAD = góc CBD = 90°. Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.
Quảng cáo
3 câu trả lời 277
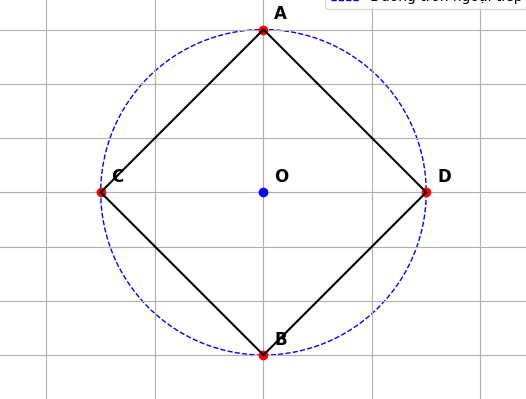
Ta có :
= 90∘ => A nằm trên đường tròn có đường kính là CD.
= 90∘ => B nằm trên đường tròn có đường kính là CD.
Vì cả hai điểm A và B đều nằm trên đường tròn có đường kính CD, nên bốn điểm A, B, C, D cùng nằm trên đường tròn đó.
= 90∘ => B nằm trên đường tròn có đường kính là CD.
Vì cả hai điểm A và B đều nằm trên đường tròn có đường kính CD, nên bốn điểm A, B, C, D cùng nằm trên đường tròn đó.
4 tháng trước
4. Kết luận:
Vì cả hai tam giác △ACD
và △BCD
đều có chung cạnh huyền CD là đường kính của đường tròn ngoại tiếp chúng, điều này có nghĩa là các điểm A, B, C, D cùng nằm trên một đường tròn có đường kính là CD.
Vậy, bốn điểm A, B, C, D cùng nằm trên một đường tròn.
Vì cả hai tam giác △ACD
và △BCD
đều có chung cạnh huyền CD là đường kính của đường tròn ngoại tiếp chúng, điều này có nghĩa là các điểm A, B, C, D cùng nằm trên một đường tròn có đường kính là CD.
Vậy, bốn điểm A, B, C, D cùng nằm trên một đường tròn.
4 tháng trước
Để chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn, ta sẽ sử dụng định lý về góc nội tiếp.
-
Xác định các góc: Theo đề bài, ta có góc CAD = 90° và góc CBD = 90°.
-
Xét tam giác ACD và BCD:
- Trong tam giác ACD, góc CAD = 90° cho thấy điểm A nằm trên đường tròn có đường kính CD.
- Tương tự, trong tam giác BCD, góc CBD = 90° cho thấy điểm B cũng nằm trên đường tròn có đường kính CD.
-
Kết luận: Vì cả hai điểm A và B đều nằm trên đường tròn có đường kính CD, nên bốn điểm A, B, C, D cùng nằm trên một đường tròn.
Vậy ta đã chứng minh được rằng bốn điểm A, B, C, D cùng nằm trên một đường tròn.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274
Gửi báo cáo thành công!


