Cho tam giác ABC vuông tại A,có đường cao AH.
a)Chứng ming rằng : tam giác ABC đồng dạng tam giác HBA ?
b)Gọi m,n lần lượt là trung điểm của BC, AB ,từ B kẻ đường thẳng vuông góc vs BC cắt MN kéo dài tại I.Chứng minh rằng : MN // AC và IB2 = IM.IN ?
Quảng cáo
4 câu trả lời 224
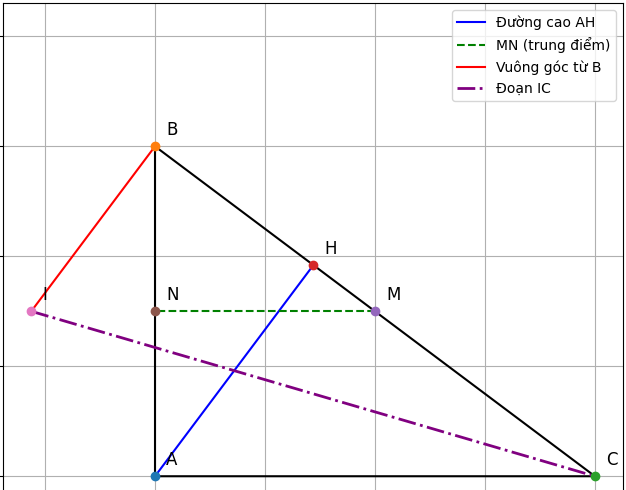
a, Chứng minh △ABC ∼ △HBA
Ta có: Tam giác ABC vuông tại A ⇒ góc A = 90∘
AH ⊥ BC (giả thiết: AH là đường cao)
Xét hai tam giác ABC và HBA:
= = 90∘ (giả thiết)
chung
=> △ABC ∼ △HBA (g.g)
N là trung điểm của cạnh AB.
M là trung điểm của cạnh BC.
Áp dụng định lý về đường trung bình của tam giác: Đường thẳng đi qua trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh thứ ba.
M là trung điểm của BC.
Đường thẳng BI BC, nên = 90∘.
Sử dụng tính chất của đường trung bình và tam giác vuông:
Xét △IBM và △INB, ta có:
.
Giải thích các bước giải:
a.Xét ΔABC,ΔHBA có:
Chung ^B
ˆBAC=ˆAHB(=90o)
→ΔABC∼ΔHBA(g.g)
b.Vì M,N là trung điểm BC,BA→MN là đường trung bình ΔABC
→MN//AC
→MN⊥AB vì AB⊥AC
→ˆINB=ˆIBM(=90o)
→ΔINB∼ΔIBM(g.g)
→IBIM=INIB
→IB2=IN.IM
c.Gọi BI∩AC=K
→MI//CK vì MN//AC
Mà M là trung điểm BC→I là trung điểm BK
→IB=IK
Ta có: AH//BK(⊥BC)
→OHIB=COCI=AOKI
→OH=OA
→O là trung điểm.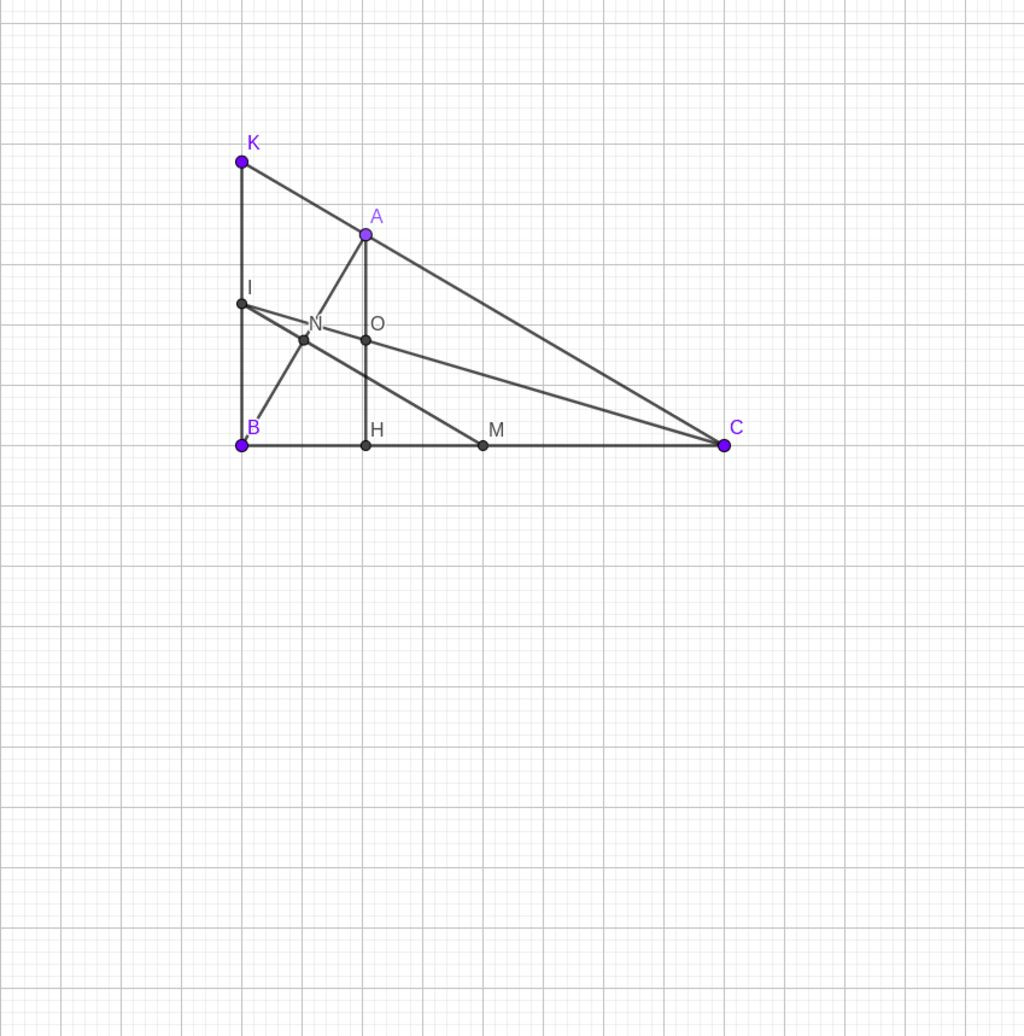
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


