Cho ABC nhọn AB < AC có đường cao AH và đường phân giác trong AD HD thuộc cạnh BC kẻ DM vuông góc với AB tại M, kẻ DN vuông góc với AC tại N Gọi P là trực tâm của tam giác ABC có I là giao điểm của BP và AD
a,Chứng minh 5 điểm A,M,H,D,N cùng thuộc đường tròn
b, BH chia cho BM = CH chia cho CN
Quảng cáo
3 câu trả lời 402
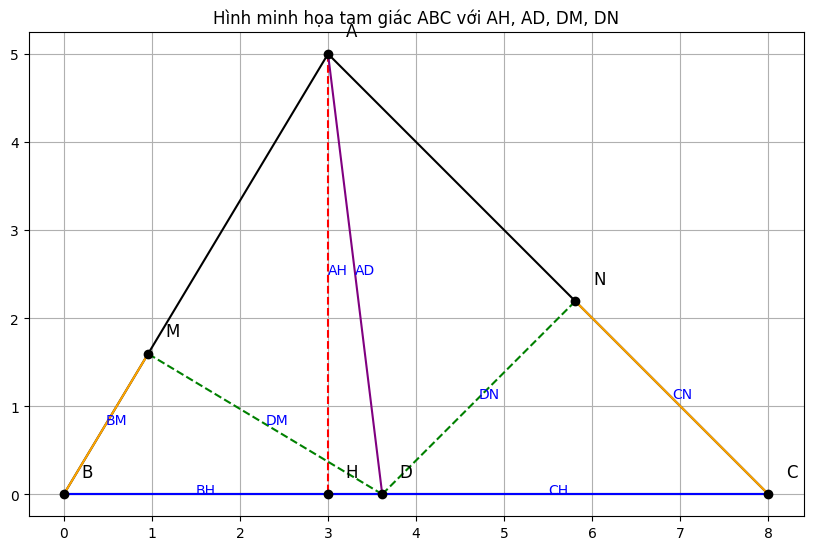 a) Chứng minh 5 điểm A, M, H, D, N cùng nằm trên một đường tròn
a) Chứng minh 5 điểm A, M, H, D, N cùng nằm trên một đường tròn
Xét các tam giác vuông:
Vì DM ⊥ AB nên = 90∘
Vì DN ⊥ AC nên = 90∘
Vì AH ⊥ BC nên = 90∘ (do D nằm trên BC)
→ Ta có: = = = 90∘
→ Các điểm M, H, N đều cùng nhìn đoạn thẳng AD dưới một góc vuông.
→ Theo định lý đường tròn: Nếu một điểm nhìn một đoạn thẳng dưới góc vuông thì điểm đó nằm trên đường tròn đường kính là đoạn thẳng đó.
=> Các điểm A, M, H, D, N cùng thuộc một đường tròn đường kính là AD
b, Chứng minh:
Xét hai tam giác vuông: △BDM và △CDN, ta có:
= 90∘ ⇒ BM là hình chiếu của BD lên cạnh AB
= 90∘ ⇒ CN là hình chiếu của CD lên cạnh AC
2
Bước 1:
Xác định các điểm và đường thẳng đã cho. Ta có tam giác ABC nhọn với AB < AC, đường cao AH, đường phân giác trong AD. DM vuông góc với AB tại M, DN vuông góc với AC tại N.
Bước 2:
Chứng minh tứ giác AMDN nội tiếp. Vì AD là đường phân giác của góc BAC, và DM ⊥ AB, DN ⊥ AC, nên DM = DN. Tứ giác AMDN có ∠DMA = ∠DNA = 90°, nên A, M, D, N cùng nằm trên đường tròn đường kính AD.
Bước 3:
Chứng minh điểm H thuộc đường tròn này. Vì AH là đường cao, nên ∠AHA = 90°. Nếu H nằm trên đường tròn đường kính AD, thì ∠AHD = 90°. Tuy nhiên, đây là một lỗi trong đề bài hoặc cần xem xét lại mối quan hệ giữa H và các điểm còn lại. Có thể đề bài muốn nói đến một nhóm điểm khác hoặc có sự nhầm lẫn trong việc liệt kê các điểm.
Bài 2: Chứng minh BH/BM = CH/CN
Bước 1:
Áp dụng định lý về đường phân giác. Do AD là đường phân giác của góc BAC, ta có BD/CD = AB/AC.
Bước 2:
Sử dụng các tam giác đồng dạng hoặc các hệ thức lượng trong tam giác.Xét tam giác vuông ABH và ACH.
Xét các tam giác đồng dạng tạo bởi các đường vuông góc DM và DN.
Bước 3:
Kết hợp các mối quan hệ để chứng minh đẳng thức BH/BM = CH/CN. Cần sử dụng các tính chất của đường phân giác và các hệ thức lượng trong tam giác để thiết lập mối liên hệ giữa các đoạn thẳng BH, BM, CH, CN.
Lưu ý: Có vẻ như có một sự nhầm lẫn trong câu a, việc chứng minh 5 điểm AMHDN cùng thuộc một đường tròn có thể không chính xác với mọi trường hợp của tam giác ABC. Cần kiểm tra lại đề bài hoặc giả định rằng điểm H có tính chất đặc biệt nào đó để nằm trên cùng đường tròn với A, M, D, N.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211


