Quảng cáo
2 câu trả lời 108
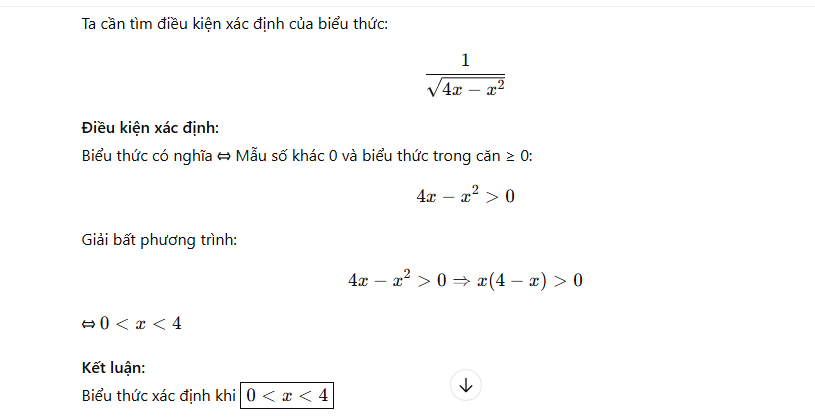
Để xác định điều kiện xác định của biểu thức 4x−x2 1, ta cần đảm bảo hai điều kiện sau:
Biểu thức dưới dấu căn phải không âm: 4x−x2≥0
Mẫu số phải khác 0: 4x−x2 =0
Phân tích và tìm điều kiện
Biểu thức dưới dấu căn lớn hơn hoặc bằng 0: 4x−x2≥0 x(4−x)≥0
Đây là một bất phương trình bậc hai. Ta xét các trường hợp:
Trường hợp 1: x≥0 và 4−x≥0 ⟹x≥0 và x≤4 ⟹0≤x≤4
Trường hợp 2: x≤0 và 4−x≤0 ⟹x≤0 và x≥4 Trường hợp này không có giá trị x nào thỏa mãn.
Vậy, điều kiện 4x−x2≥0 tương đương với 0≤x≤4.
Mẫu số khác 0: 4x−x2 =0 ⟹4x−x2=0 ⟹x(4−x)=0 ⟹x=0 và 4−x=0 ⟹x=0 và x=4
Kết hợp các điều kiện
Kết hợp cả hai điều kiện trên, ta có:
0≤x≤4
x=0
x=4
Do đó, x phải lớn hơn 0 và nhỏ hơn 4.
Điều kiện xác định của biểu thức là: 0<x<4.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211