Bước 1: Phân tích hình học
Về các điểm:
Vì AD là đường cao, nên D ∈ BC và AD ⊥ BC.
BE là đường cao, nên E ∈ AC và BE ⊥ AC.
H là giao điểm hai đường cao → H là trực tâm của tam giác ABC.
Đường tròn (O) có đường kính AH nên mọi điểm nằm trên đường tròn và tạo góc vuông tại tiếp điểm với AH.

Bước 2: Chứng minh DE là tiếp tuyến
Ý tưởng chính:
Ta sẽ chứng minh rằng góc giữa đường thẳng DE và bán kính OH tại tiếp điểm là 90°, tức là OH ⊥ DE, vậy DE là tiếp tuyến tại điểm D.

Nhưng vì đường tròn có đường kính AH, nên một điểm bất kỳ nằm trên đường tròn thỏa mãn:

Một tam giác nội tiếp có một cạnh là đường kính thì góc đối diện cạnh đó là góc vuông.
Do đó, nếu điểm D nằm trên đường tròn đường kính AH, và ta chứng minh góc D nằm trong tam giác vuông tạo bởi AH, thì ta có thể chứng minh tam giác nào đó vuông tại D, từ đó suy ra DE tiếp xúc đường tròn tại D.

Tuy nhiên, ta dùng cách khác hiệu quả hơn:

Cách chứng minh hình học chính xác:
1. Gọi O là tâm đường tròn đường kính AH
Do AH là đường kính ⇒ O là trung điểm của AH.
Đường tròn tâm O, bán kính R=$\frac{AH}{2}$

2. Chứng minh góc $\widehat{ODE}={90}^o$
Nếu ta chứng minh OD ⊥ DE thì DE là tiếp tuyến tại điểm D của đường tròn (O).
3. Quan sát:
D nằm trên đường cao từ A ⇒ AD ⊥ BC.
E nằm trên đường cao từ B ⇒ BE ⊥ AC.
H là trực tâm ⇒ AH ⊥ BC, và BH ⊥ AC.
Vì D ∈ BC và E ∈ AC, ta xét tứ giác ADEH để chứng minh góc tại D là vuông.

Thay vì góc, ta dùng tích vô hướng hoặc vector để chứng minh góc giữa bán kính và tiếp tuyến là 90°.

Chứng minh bằng tính chất hình học thuần túy:
Xét đường tròn (O) đường kính AH:

Gọi M∈(O) , khi và chỉ khi $\widehat{AMH}={90}^o$
Ta chứng minh rằng $\widehat{ADE}={90}^o$ ⇒ D nằm trên đường tròn (O).
Góc ADE = 90°?
D nằm trên BC và AD ⊥ BC ⇒ AD là đường cao.
E nằm trên AC và BE ⊥ AC ⇒ BE là đường cao.
H là giao điểm 2 đường cao ⇒ AH ⊥ BC.
=> $\widehat{ADE}={90}^o$

Vậy:

Điểm D thuộc (O) vì $\widehat{ADE}={90}^o$
Vậy đường thẳng DE vuông góc với bán kính OD tại điểm D
→ Theo định nghĩa: DE là tiếp tuyến của đường tròn (O) tại D

✅ Kết luận:
DE là tiếp tuyến của đường tròn (O) đường kính AH tại D.

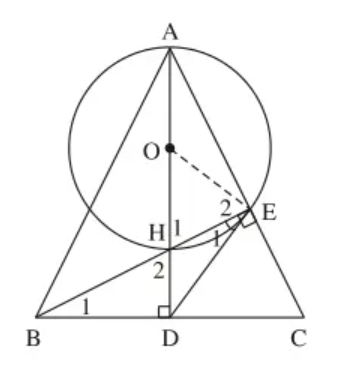
  Gọi O là trung điểm của AH

Tam giác AEH vuông tại E có EO là đường trung tuyến nên :

EO=OA=OH=AH2EO=OA=OH=AH2 (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

Do đó, điểm E nằm trên đường tròn (O;AH2)O;AH2

Ta có: OH = OE

Do đó, tam giác OHE cân tại O

⇒ˆOEH=ˆOHE⇒OEH^=OHE^ (1)

Mà ˆBHD=ˆOHEBHD^=OHE^ (là hai góc đối đỉnh) (2)

Xét tam giác BHD có:

ˆHDB=90oHDB^=90o

⇒ˆHBD+ˆBHD=90o⇒HBD^+BHD^=90o (3)

Từ (1), (2), (3) ta suy ra: ˆOEH+ˆHBD=90oOEH^+HBD^=90o (4)

Xét tam giác ABC cân tại A

Có AD là đường cao cũng là đường trung tuyến

Do đó, D là trung điểm của BC

⇒BD=CD=BC2⇒BD=CD=BC2

Xét tam giác BCE vuông tại E có ED là đường trung tuyến nên:

ED=BD=DC=BC2ED=BD=DC=BC2 (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

Do đó, tam giác BDE cân tại D

⇒ˆDBE=ˆDEB⇒DBE^=DEB^ (5)

Từ (4) và (5) ta suy ra:

ˆOEH+ˆDEB=ˆBHD+ˆDBH=90o⇒ˆDEO=90oOEH^+DEB^=BHD^+DBH^=90o⇒DEO^=90o

⇒DE⊥EO⇒DE⊥EO

Vậy DE là tiếp tuyến của đường tròn (O).a)