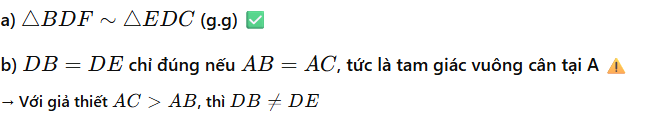Question

Đã trả lời bởi chuyên gia

Answer 1

Chúng ta có tam giác ABC vuông tại A và AD là đường phân giác của góc A, nghĩa là góc BAD = góc CAD.

1. **Chứng minh tam giác BDF đồng dạng với tam giác EDC**:

Ta sẽ chỉ ra rằng các góc của hai tam giác này bằng nhau:

- **Xét tam giác BDF**:
- Góc BDF là góc ngoài của tam giác ABC tại B, do đó:
\[
\angle BDF = \angle C
\]
- Góc BFD là góc tạo bởi đường phân giác AD chia góc A ra thành hai phần bằng nhau, cho nên:
\[
\angle BFD = \angle BAD = \angle CAD
\]

- **Xét tam giác EDC**:
- Góc EDC là góc tại D, do AD là đường phân giác nên:
\[
\angle EDC = \angle CAD
\]

Khi đó, ta có:
- \(\angle BDF = \angle EDC\) (góc cùng lớn C)
- \(\angle BFD = \angle CAD\) (góc phân giác)

Như vậy, ta có thể kết luận:
\[
\triangle BDF \sim \triangle EDC \quad \text{(theo trường hợp góc-góc)}
\]

2. **Chứng minh DB = DE**:

Từ tính đồng dạng của hai tam giác, ta có tỉ số các cạnh tương ứng. Từ \(\triangle BDF \sim \triangle EDC\), ta có:
\[
\frac{BD}{DE} = \frac{BF}{EC}
\]
Do FD là đường vuông góc với BC và D là điểm nằm trên BC, nên ta có:
- EC là phần chiếu từ C xuống đường DF, nó được xem như là chiều cao từ C trong góc vuông ABC, với A,D thuộc đường phân giác, do đó EC = BF.

Do đó, từ đồng dạng, ta thấy:
\[
BD = DE
\]

Cuối cùng, từ hai chứng minh trên, ta có:
- a) \(\triangle BDF\) đồng dạng với \(\triangle EDC\)
- b) \(DB = DE\)

Thay vì là những chứng minh giải thích, các bạn cần có hình vẽ minh họa thêm.

...Xem thêm

Answer 2