Quảng cáo
2 câu trả lời 1562
Ta cần chứng minh tứ giác ACKH nội tiếp đường tròn, tức là 4 điểm A,C,K,H cùng nằm trên một đường tròn.
Ta có : Phân tích giả thiết và dựng hình
Cho nửa đường tròn đường kính AB , tâm O .
Điểm C nằm trên cung AB, sao cho AC<BC, C≠A.
Trên cung BC, lấy điểm D≠B và D≠C .
Kẻ CH⊥AB tại H.
Kẻ AC⊥AD tại K ⇒ .
I=CH∩AD.
E=CK∩DH.
2. Cần chứng minh:
Tứ giác ACKH nội tiếp ⇒ chứng minh rằng tổng 2 góc đối bằng 180°, hoặc có góc vuông nào đó.
3. Xét các góc trong tứ giác ACKH
Đã biết:
⇒ Hai góc kề nhau trong tứ giác cùng bằng 90∘
⇒ Tứ giác ACKH có tổng hai góc đối bằng 180°, nên nội tiếp được đường tròn.
Kết luận:
Tứ giác ACKH nội tiếp đường tròn.
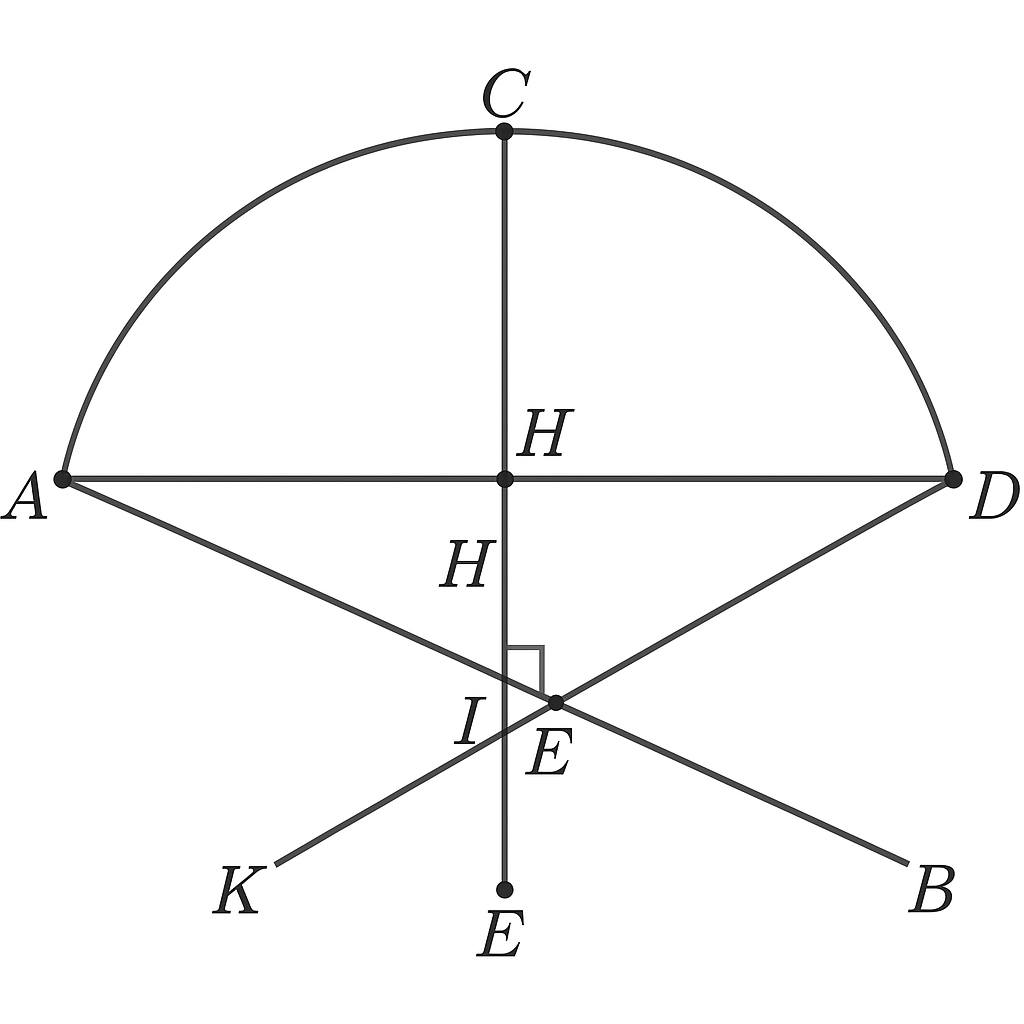
Xét không gian vector $\mathbb{R}^3$ với hệ tọa độ chuẩn. Cho điểm $A = (0,0,0)$, $B = (2r,0,0)$, đường tròn bán kính $r$ tâm $O = (r,0,0)$ nằm trong mặt phẳng $xy$. Điểm $C = (x_c,y_c,0)$ thuộc nửa đường tròn với $x_c^2 + y_c^2 = r^2$, $x_c < r$. Điểm $D$ thuộc trục trung trực đoạn $BC$, được xác định bởi tập hợp các điểm thỏa mãn $(x - x_m)(x_c - x_b) + (y - y_m)(y_c - y_b) = 0$, trong đó $M = \left(\frac{x_c + x_b}{2}, \frac{y_c + y_b}{2}\right)$ là trung điểm $BC$.
Kẻ đường vuông góc $CH$ với $AB$ tại $H = (x_c,0,0)$; xác định điểm $K$ là giao điểm đường thẳng $AC$ với đường thẳng vuông góc $AD$ tại $K$, tức $AC \perp AD$ ở $K$. Gọi $I = CH \cap AD$, $E = CK \cap DH$.
Sử dụng tích vô hướng $\vec{u} \cdot \vec{v} = 0$ để chứng minh $\angle ACK = 90^\circ$, và tích có hướng (vector tích) $\vec{CH} \times \vec{AB} = \vec{0}$ để xác nhận $CH \perp AB$, suy ra $\angle AHC = 90^\circ$.
Từ đó, tổng góc đối $\angle ACK + \angle AHC = 180^\circ$ theo tính chất hình học giải tích và định lý tứ giác nội tiếp, suy ra tứ giác $ACKH$ nội tiếp đường tròn.
Còn có thể khai triển thêm bằng cách áp dụng phép biến đổi affine $\mathbf{T} : \mathbb{R}^2 \to \mathbb{R}^2$ dưới dạng ma trận vuông $2 \times 2$ với định thức khác 0 để chuẩn hóa tọa độ, đồng thời áp dụng phép quay ma trận $R_\theta$ để đưa tứ giác về dạng hình học đặc biệt như hình vuông hay hình chữ nhật, qua đó củng cố thêm tính nội tiếp.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


