Cho hàm số y=2x2 có đồ thị (p)
a .vẽ đồ thị (p)
b . bằng phép tính tìm tọa độ giao điểm của (p) và đường thẳng (d) y=-x+6
Quảng cáo
2 câu trả lời 181
Để vẽ đồ thị (P), ta cần xác định một số điểm thuộc đồ thị. Ta có thể lập bảng giá trị như sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y=2x2 | 8 | 2 | 0 | 2 | 8 |
Sau khi có các điểm này, bạn có thể vẽ đồ thị (P) trên hệ trục tọa độ Oxy. Đồ thị sẽ là một parabol có đỉnh tại gốc tọa độ (0, 0) và hướng lên trên.
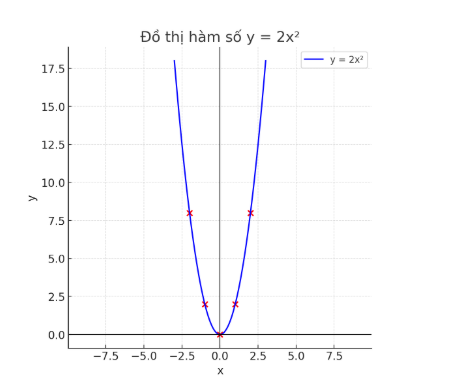
b. Tìm tọa độ giao điểm của (P) và đường thẳng (D): y=−x+6
Để tìm tọa độ giao điểm, ta giải phương trình hoành độ giao điểm bằng cách cho hai biểu thức của y bằng nhau:
2x2=−x+6
Chuyển vế để đưa về phương trình bậc hai:
2x2+x−6=0
Giải phương trình bậc hai này, ta có thể sử dụng công thức nghiệm hoặc phân tích thành nhân tử. Ở đây, ta sẽ phân tích thành nhân tử:
2x2+4x−3x−6=0
1. 2x−3=0⇒x=
2. x+2=0⇒x=−2
Tiếp theo, ta tìm giá trị y tương ứng với mỗi giá trị x bằng cách thay vào phương trình của đường thẳng (D):
1. Với x=, y=−+6=
2. Với x=−2, y=−(−2)+6=8
Vậy tọa độ giao điểm của (P) và (D) là:
1.
Kết luận:
Đồ thị (P) y=2x2 là một parabol có đỉnh tại (0, 0) và hướng lên trên.
Tọa độ giao điểm của (P) và (D) là
Cho hàm số $y = 2x^3$ có đồ thị $(p)$.\\
Tìm tọa độ giao điểm của $(p)$ và đường thẳng $(d): y = -x + 6$.\\
Phương trình giao điểm thỏa hệ:\\
$
\begin{cases}
y = 2x^3, \\
y = -x + 6
\end{cases}
\implies 2x^3 = -x + 6 \implies 2x^3 + x - 6 = 0.
$\\
Đặt hàm $f(x) = 2x^3 + x - 6$.\\
Ta có đạo hàm $f'(x) = 6x^2 + 1 > 0, \forall x \in \mathbb{R}$,\\
suy ra $f$ đơn điệu tăng trên $\mathbb{R}$, nên phương trình $f(x)=0$ có duy nhất một nghiệm thực.\\
Thử nghiệm:\\
$f(1) = 2 + 1 - 6 = -3 < 0$,\\
$f(2) = 16 + 2 - 6 = 12 > 0$.\\
Nghiệm nằm trong $(1, 2)$.\\
Dùng phương pháp Newton với $x_0 = 1.5$: \\
$f(1.5) = 2(3.375) + 1.5 - 6 = 2.25$,\\
$f'(1.5) = 14.5$,\\
$x_1 = 1.5 - \frac{2.25}{14.5} \approx 1.345$.\\
Tiếp tục:\\
$f(1.345) \approx 0.32$, $f'(1.345) \approx 11.85$,\\
$x_2 = 1.345 - \frac{0.32}{11.85} \approx 1.318$.\\
Nghiệm gần đúng: $x_0 \approx 1.318$,\\
Tọa độ giao điểm là: \\
$\boxed{\left(1.318; 2 \times (1.318)^3 \approx 4.58\right)}$.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211


