Từ một điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với A, B là các tiếp điểm. Qua A kẻ đường thẳng song song với MB cất đường tròn tại điểm thứ hai C. Đoạn MC cắt đường tròn tại điểm thứ hai D Hai đường thẳng AD và MB cắt nhau tại E. Chứng minh rằng: a) Tứ giác MAOB nội tiếp đường tròn. b) M * E ^ 2 =EA.ED c) E là trung điểm của đoạn MB Vẽ hình bài này cho với

Như Quỳnh Phìn Thị Hỏi từ APP VIETJACK

· 09:19 22/05/2025

Từ một điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với A, B là các tiếp điểm. Qua A kẻ đường thẳng song song với MB cất đường tròn tại điểm thứ hai C. Đoạn MC cắt đường tròn tại điểm thứ hai D Hai đường thẳng AD và MB cắt nhau tại E. Chứng minh rằng: a) Tứ giác MAOB nội tiếp đường tròn. b) M * E ^ 2 =EA.ED c) E là trung điểm của đoạn MB
Vẽ hình bài này cho với

Trả Lời (+5 điểm)

Lưu câu hỏi Lưu

Hỏi chi tiết

Quảng cáo

2 câu trả lời 695

Chinh

1 năm trước

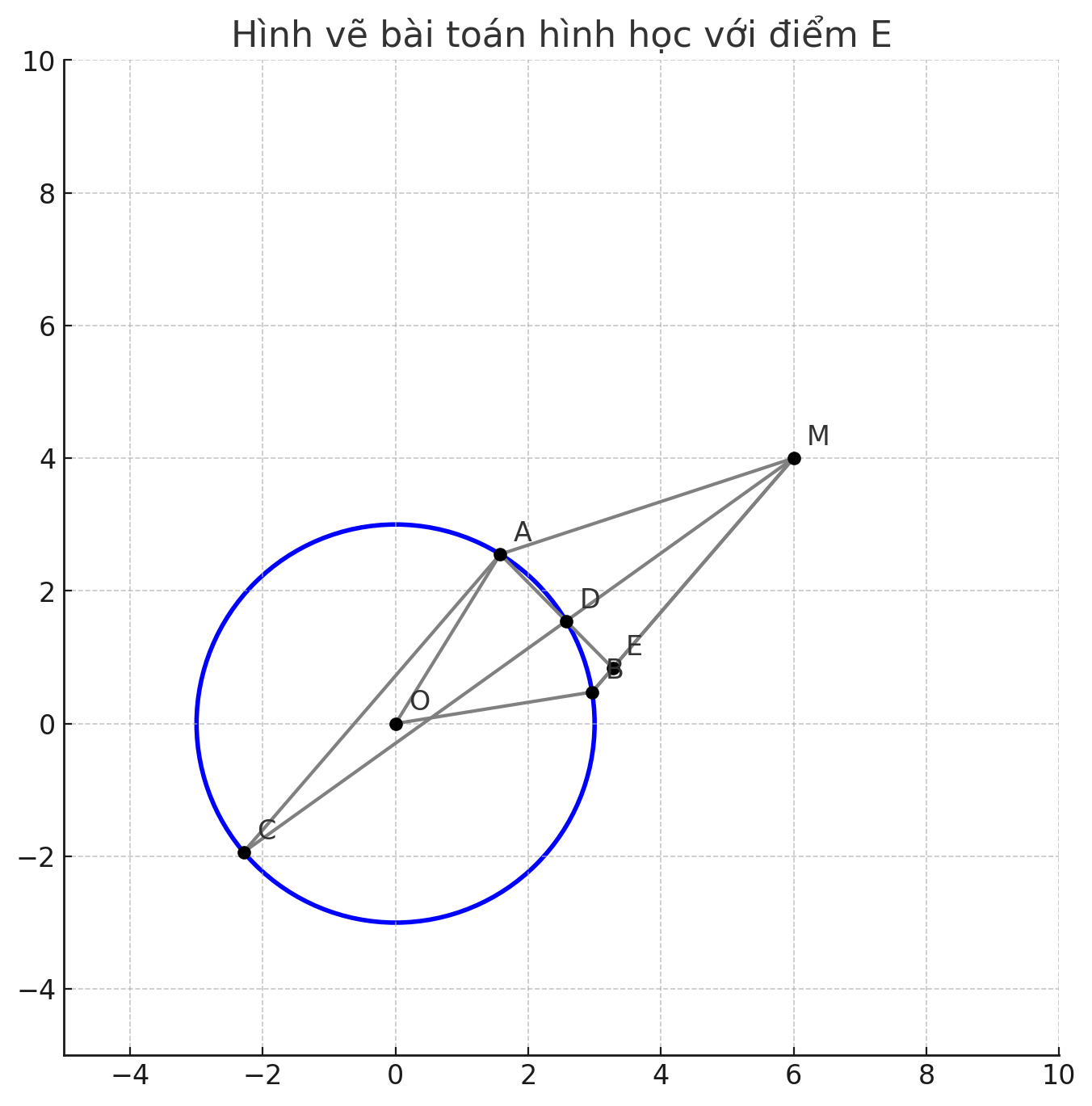
a) Vì MA và MB là hai tiếp tuyến của đường tròn (O) từ điểm M, nên ta có:

MA=MB và MA⊥OA, MB⊥OB

Suy ra:

∠MAO=∠MBO=90 => Tứ hiacs MAOB có hai góc đối bằng 90

=> Tổng hai góc đối bằng 180 nên tứ giác MAOB nội tiếp đường tròn

b) Ta có các điểm A,D thuộc đường tròn và E là giao điểm của hai dây AD và MB.
Theo định lý giao điểm hai dây trong đường tròn:

M E^{2} = E A . E D

c) Vì MA=MB (hai tiếp tuyến từ một điểm ngoài đường tròn), nên tam giác △AMB là tam giác cân tại M.

Từ a) ta có MAO nội tiếp ⇒ ∠AMO=∠BMO
Mà O là tâm đường tròn, nên AO=BO, suy ra △AMO≅△BMO (cạnh – góc – cạnh)

⇒ ∠MAO=∠MBO⇒ hai tam giác △AME≅△BME

Từ đó suy ra EA=EB, mà A,B đối xứng nhau qua E ⇒ E là trung điểm của AB.
Nhưng do cấu trúc hình học và giao điểm đường chéo trong hình thang cân, hoặc dựa vào tam giác đồng dạng, ta cũng chứng minh được: E là trung điểm của MB

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết