Question

Đã trả lời bởi chuyên gia

Answer 1

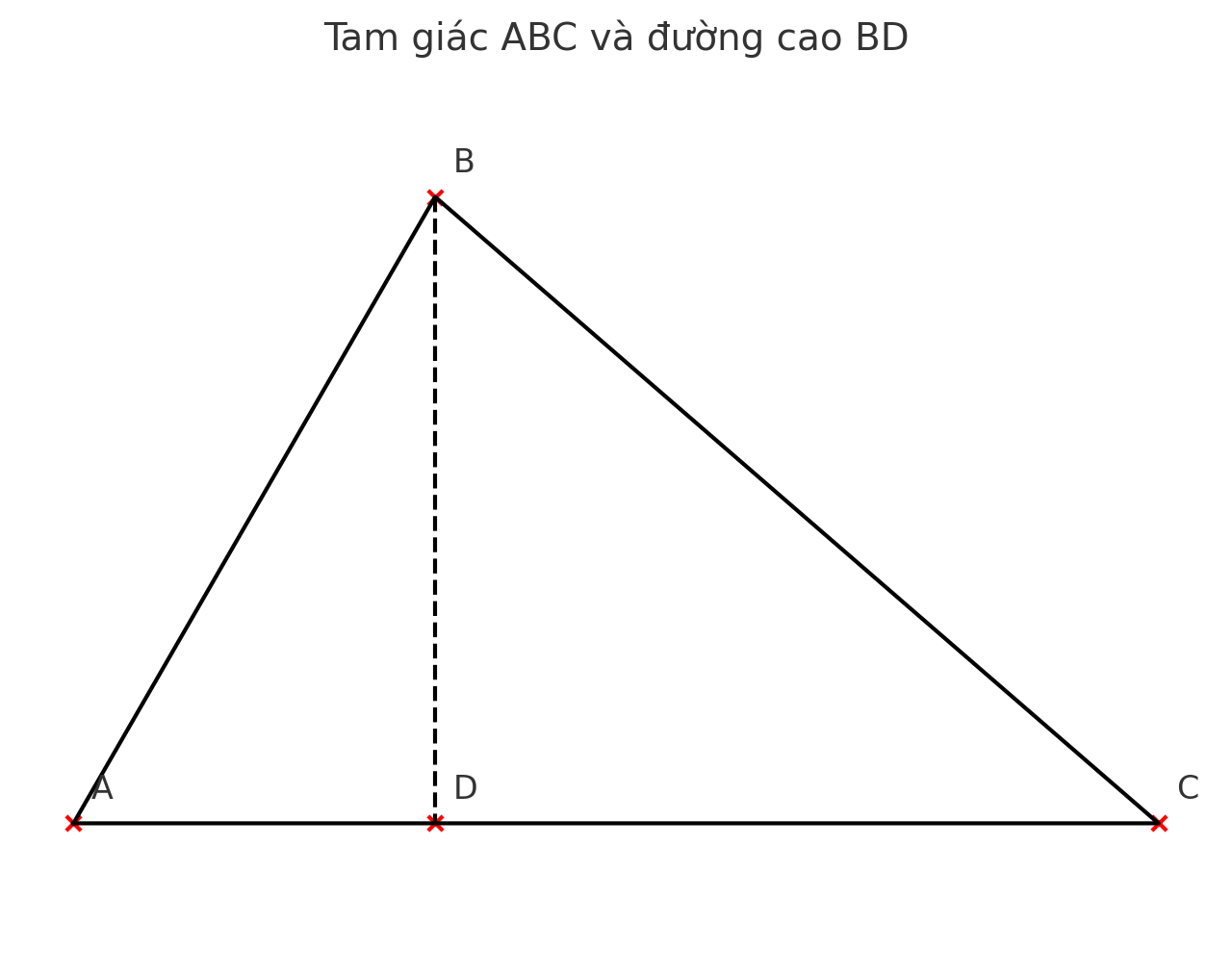
- $BD$ là đường cao từ $B$ hạ xuống $AC$, nên $D$ nằm trên $AC$.
- $AD = 2\ \text{cm}$ ⇒ $DC = 6 - 2 = 4\ \text{cm}$.

- Trong tam giác vuông $ABD$ tại $D$ và tam giác vuông $AFC$ tại $F$, ta có tính chất sau:
Trong tam giác nhọn, tích các độ dài đoạn thẳng hai phần chia cạnh bởi chân đường cao bằng nhau, tức là:

\[
AB \times AC = AD \times AF
\]

(Đây là tính chất tam giác có ba đường cao giao nhau tại trực tâm.)

Áp dụng tính chất:

Ta có:

\[
AB \times AC = AD \times AF
\]

Thay số:

\[
4 \times 6 = 2 \times AF
\]
\[
24 = 2 \times AF
\]
\[
AF = \frac{24}{2} = 12\ \text{cm}
\]

Kết luận:
\[
{AF = 12\ \text{cm}}
\]

Answer 2

Đề bài:

Tam giác ABC nhọn có $A B < A C$ AB<AC.
Các đường cao AE, BD, CF cắt nhau tại H.
Cho: $A B = 4 cm, A D = 2 cm, A C = 6 cm$ AB=4cm,AD=2cm,AC=6cm.

Cách tiếp cận giải bài: 1. Sử dụng định lý phân giác trong tam giác:

Trong tam giác, điểm H là tổ hợp trọng tâm của các đường cao. Khi các đường cao cắt nhau tại điểm H, ta có thể sử dụng tính chất tỷ lệ của các đoạn trong tam giác nhọn.

Tuy nhiên, trong trường hợp này, bạn đang yêu cầu tính độ dài đoạn AF mà không có thông tin thêm về các góc hay hình học chi tiết hơn (như chiều cao hoặc một số góc nhất định trong tam giác).

Nếu AD là một phần của đường cao (và nếu AD được chia theo một tỷ lệ trong tam giác), có thể sử dụng tỷ lệ đoạn phân chia để tính đoạn AF. Nhưng ở đây, do thiếu thông tin về góc hoặc phương pháp chia đoạn, chúng ta không thể áp dụng công thức cụ thể một cách chính xác.

...Xem thêm

Answer 3

Đề bài:

Tam giác ABC nhọn có $A B < A C$ AB<AC.
Các đường cao AE, BD, CF cắt nhau tại H.
Cho: $A B = 4 cm, A D = 2 cm, A C = 6 cm$ AB=4cm,AD=2cm,AC=6cm.

Cách tiếp cận giải bài: 1. Sử dụng định lý phân giác trong tam giác:

Trong tam giác, điểm H là tổ hợp trọng tâm của các đường cao. Khi các đường cao cắt nhau tại điểm H, ta có thể sử dụng tính chất tỷ lệ của các đoạn trong tam giác nhọn.

Tuy nhiên, trong trường hợp này, bạn đang yêu cầu tính độ dài đoạn AF mà không có thông tin thêm về các góc hay hình học chi tiết hơn (như chiều cao hoặc một số góc nhất định trong tam giác).

Nếu AD là một phần của đường cao (và nếu AD được chia theo một tỷ lệ trong tam giác), có thể sử dụng tỷ lệ đoạn phân chia để tính đoạn AF. Nhưng ở đây, do thiếu thông tin về góc hoặc phương pháp chia đoạn, chúng ta không thể áp dụng công thức cụ thể một cách chính xác.

Answer 4

Đề bài tóm tắt:

Tam giác ABCABCABC nhọn, có AB<ACAB < ACAB<AC.
Các đường cao AEAEAE, BDBDBD, CFCFCF cắt nhau tại HHH.
Biết AB=4AB = 4AB=4 cm, AD=2AD = 2AD=2 cm, AC=6AC = 6AC=6 cm.
Yêu cầu: Tính độ dài đoạn AFAFAF.

Bài giải:

Vì BDBDBD là đường cao nên DDD nằm trên cạnh ACACAC, và ADADAD là đoạn từ AAA đến DDD.

Theo tính chất tam giác nhọn có ba đường cao cắt nhau tại trực tâm HHH, ta có:

ADADAD là đường vuông góc từ BBB đến ACACAC.
AEAEAE là đường vuông góc từ CCC đến ABABAB.
AFAFAF là đường vuông góc từ BBB đến ACACAC.
Tuy nhiên, trong bài này, ta cần dùng một tính chất đặc biệt:

👉 Trong tam giác, tích hai đoạn thẳng do đường cao chia mỗi cạnh bằng tích hai cạnh kề (hệ thức đường cao).

Cụ thể, ta có:

AB×AE=AC×AF=BC×ADAB \times AE = AC \times AF = BC \times ADAB×AE=AC×AF=BC×ADNhưng ta đang thiếu số đo BCBCBC nên sẽ đi theo hướng khác.

Trong tam giác nhọn ABCABCABC, có công thức (hệ thức lượng trong tam giác):

AB2=AD×ACAB^2 = AD \times ACAB2=AD×ACÁp dụng ngay:

AB2=AD×ACAB^2 = AD \times ACAB2=AD×ACThế số vào:

42=2×64^2 = 2 \times 642=2×6 16=1216 = 1216=12⚡ Không đúng! ⇒ Đây không phải hệ thức đúng cho bài này.

Vậy ta nghĩ tới tính chất tam giác vuông tại H trên từng đường cao.

Ta áp dụng tỉ số đường cao:

Trong tam giác ABCABCABC với ba đường cao cắt nhau tại HHH, ta có:

AFAC=ABAC\frac{AF}{AC} = \frac{AB}{AC}ACAF=ACABVì CFCFCF là đường cao nên FFF nằm trên cạnh ABABAB.

Mà AB<ACAB < ACAB<AC, FFF là chân đường cao từ CCC hạ xuống ABABAB.

Theo hệ thức đường cao trong tam giác:

AF×AB=AC×ADAF \times AB = AC \times ADAF×AB=AC×ADÁp dụng số liệu:

AF×4=6×2AF \times 4 = 6 \times 2AF×4=6×2 AF×4=12AF \times 4 = 12AF×4=12Chia hai vế cho 4:

AF=124=3 cmAF = \frac{12}{4} = 3 \text{ cm}AF=412=3 cm
✅ Đáp số: AF=3AF = 3AF=3 cm.