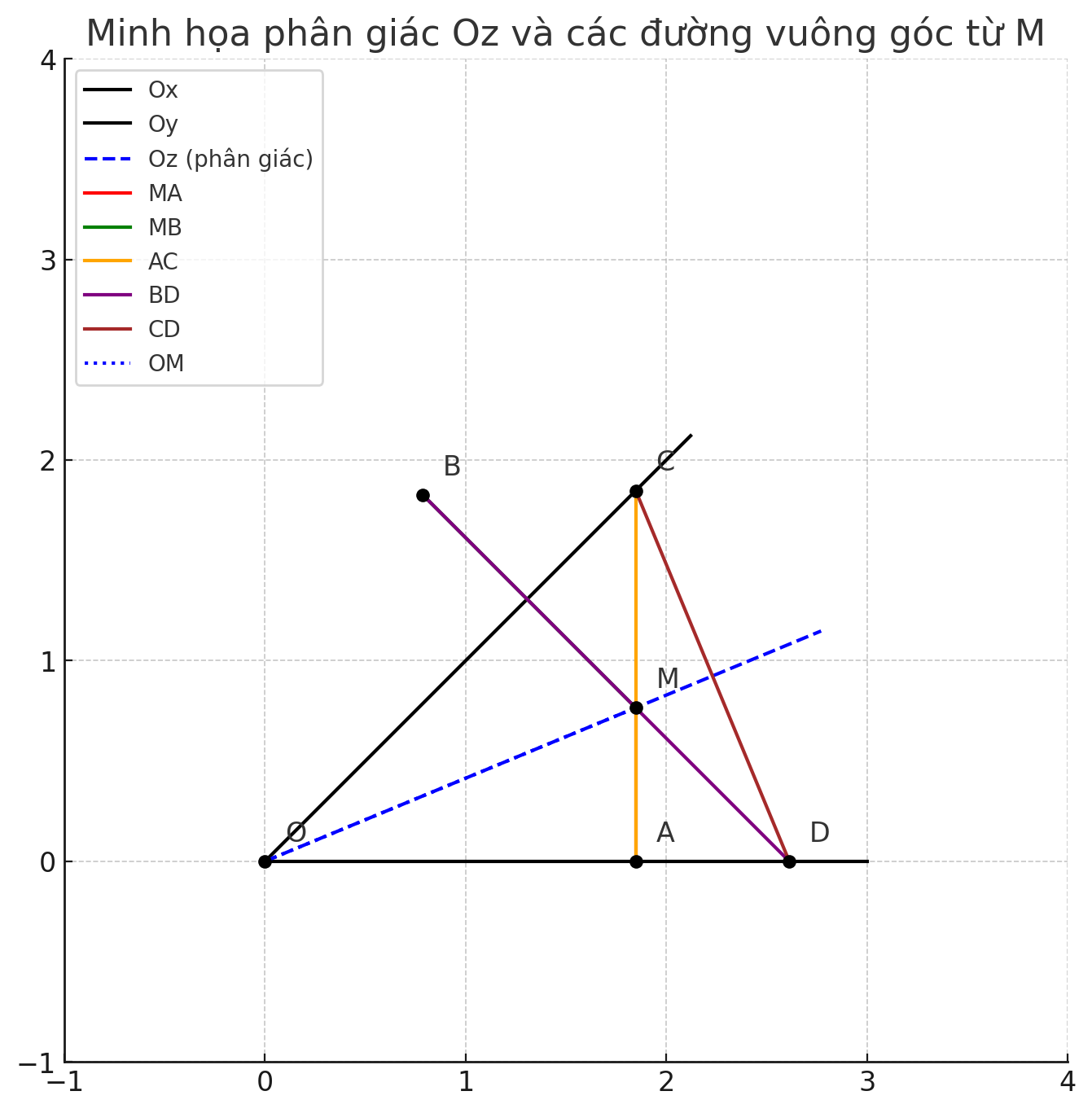
🎯 Dữ kiện:
∠xOy\angle xOy∠xOy là góc nhọn.
OzOzOz là phân giác của góc xOyxOyxOy.
M∈OzM \in OzM∈Oz, M≠OM \ne OM=O.
Qua MMM vẽ:

đường thẳng a vuông góc Ox tại A, cắt OyOyOy tại CCC
đường thẳng b vuông góc Oy tại B, cắt OxOxOx tại DDD

✅ Câu A: Chứng minh MA=MBMA = MBMA=MB
✏️ Lập luận:
OzOzOz là phân giác ⇒ ∠MOx=∠MOy\angle MOx = \angle MOy∠MOx=∠MOy
MA⊥OxMA \perp OxMA⊥Ox, ⇒ ∠MAO=90∘\angle MAO = 90^\circ∠MAO=90∘
MB⊥OyMB \perp OyMB⊥Oy, ⇒ ∠MBO=90∘\angle MBO = 90^\circ∠MBO=90∘
Xét 2 tam giác vuông:
Tam giác △MAO\triangle MAO△MAO vuông tại AAA
Tam giác △MBO\triangle MBO△MBO vuông tại BBB
Hai tam giác này có:

∠OMA=∠OMB\angle OMA = \angle OMB∠OMA=∠OMB (vì OzOzOz là phân giác)
∠MAO=∠MBO=90∘\angle MAO = \angle MBO = 90^\circ∠MAO=∠MBO=90∘
Chung cạnh OMOMOM
➡️ Tam giác △MAO\triangle MAO△MAO bằng tam giác △MBO\triangle MBO△MBO theo góc – cạnh – góc (g.c.g)

⇒MA=MB\Rightarrow MA = MB⇒MA=MB✅ Đpcm

✅ Câu B: Chứng minh DM+AM<DCDM + AM < DCDM+AM<DC
✏️ Phân tích:
Ta có:

A∈OxA \in OxA∈Ox, C∈OyC \in OyC∈Oy, và AC⊥OxAC \perp OxAC⊥Ox
B∈OyB \in OyB∈Oy, D∈OxD \in OxD∈Ox, và BD⊥OyBD \perp OyBD⊥Oy
Xét tứ giác ADCMADCMADCM, ta muốn chứng minh:

DM+AM<DCDM + AM < DCDM+AM<DCTa biết từ câu A:

MA=MBMA = MBMA=MB
MB⊥OyMB \perp OyMB⊥Oy, nên MB<CBMB < CBMB<CB (trừ khi MMM nằm đúng trên đường thẳng vuông góc đi qua CCC, điều không xảy ra với mọi MMM)
Do đó, đường gãy D→M→AD \to M \to AD→M→A sẽ ngắn hơn đường thẳng D→CD \to CD→C
Hoặc xét theo bất đẳng thức tam giác trong tam giác △DMC\triangle DMC△DMC:

DM+MC>DC⇒DM+AM<DC(vıˋ AM < MC)DM + MC > DC \Rightarrow DM + AM < DC \quad \text{(vì AM < MC)}DM+MC>DC⇒DM+AM<DC(vıˋ AM < MC)✅ Đpcm

✅ Câu C: Chứng minh OM⊥CDOM \perp CDOM⊥CD
✏️ Phân tích:
Ta cần chứng minh OM⊥CDOM \perp CDOM⊥CD

Xét các yếu tố:

OzOzOz là phân giác của góc xOyxOyxOy
M∈OzM \in OzM∈Oz, tức là điểm nằm trên phân giác
MA⊥OxMA \perp OxMA⊥Ox, MB⊥OyMB \perp OyMB⊥Oy
A∈OxA \in OxA∈Ox, B∈OyB \in OyB∈Oy, từ đó kéo dài tạo thành hình thang
Từ câu A: MA=MBMA = MBMA=MB, nên điểm MMM cách đều hai trục OxOxOx và OyOyOy

➡️ Đường thẳng CDCDCD nối hai điểm C∈OyC \in OyC∈Oy, D∈OxD \in OxD∈Ox

Vì CCC và DDD được tạo từ hai đường thẳng qua MMM vuông góc với Ox và Oy, và do M∈M \inM∈ phân giác ⇒ thì đường thẳng CDCDCD sẽ vuông góc với phân giác OMOMOM

Hay nói cách khác, phân giác của góc nhọn tạo thành bởi hai trục Ox, Oy sẽ vuông góc với dây CD khi CD nối hai điểm từ vuông góc thả từ M.

✅ Vậy OM⊥CDOM \perp CDOM⊥CD
(hoặc: tam giác vuông cân, nên phân giác vuông góc với cạnh đáy — suy ra trực tiếp)

✅ Kết luận:
a) MA=MBMA = MBMA=MB
b) DM+AM<DCDM + AM < DCDM+AM<DC
c) OM⊥CDOM \perp CDOM⊥CD