Quảng cáo
3 câu trả lời 561
Xét tam giác DHC và NHB
Ta sẽ chứng minh 2 tam giác này đồng dạng theo trường hợp góc - góc (g.g).
- Xét \( \angle DHC \) và \( \angle NHB \).
Ta có:
- \( \angle DHC \) là góc tại H của tam giác DHC.
- \( \angle NHB \) là góc tại H của tam giác NHB.
⇒ Chúng có chung góc tại đỉnh H, ta gọi là \( \angle H \).
- Vì \( BH ⊥ CM \) → \( \angle BH(CM) = 90^\circ \)
- \( HN ⊥ DH \) ⇒ \( \angle HNB = 90^\circ \) (N là hình chiếu vuông góc từ H xuống DH)
→ Như vậy:
- Tam giác DHC có góc vuông tại H (do BH ⊥ CM, mà C thuộc CM).
- Tam giác NHB có góc vuông tại N (HN ⊥ DH).
→ 2 tam giác đều có 1 góc vuông, và có góc tại H chung ⇒ đồng dạng theo góc – góc (g.g).
\[
\boxed{\triangle DHC \sim \triangle NHB \text{ (g.g)}}
\]
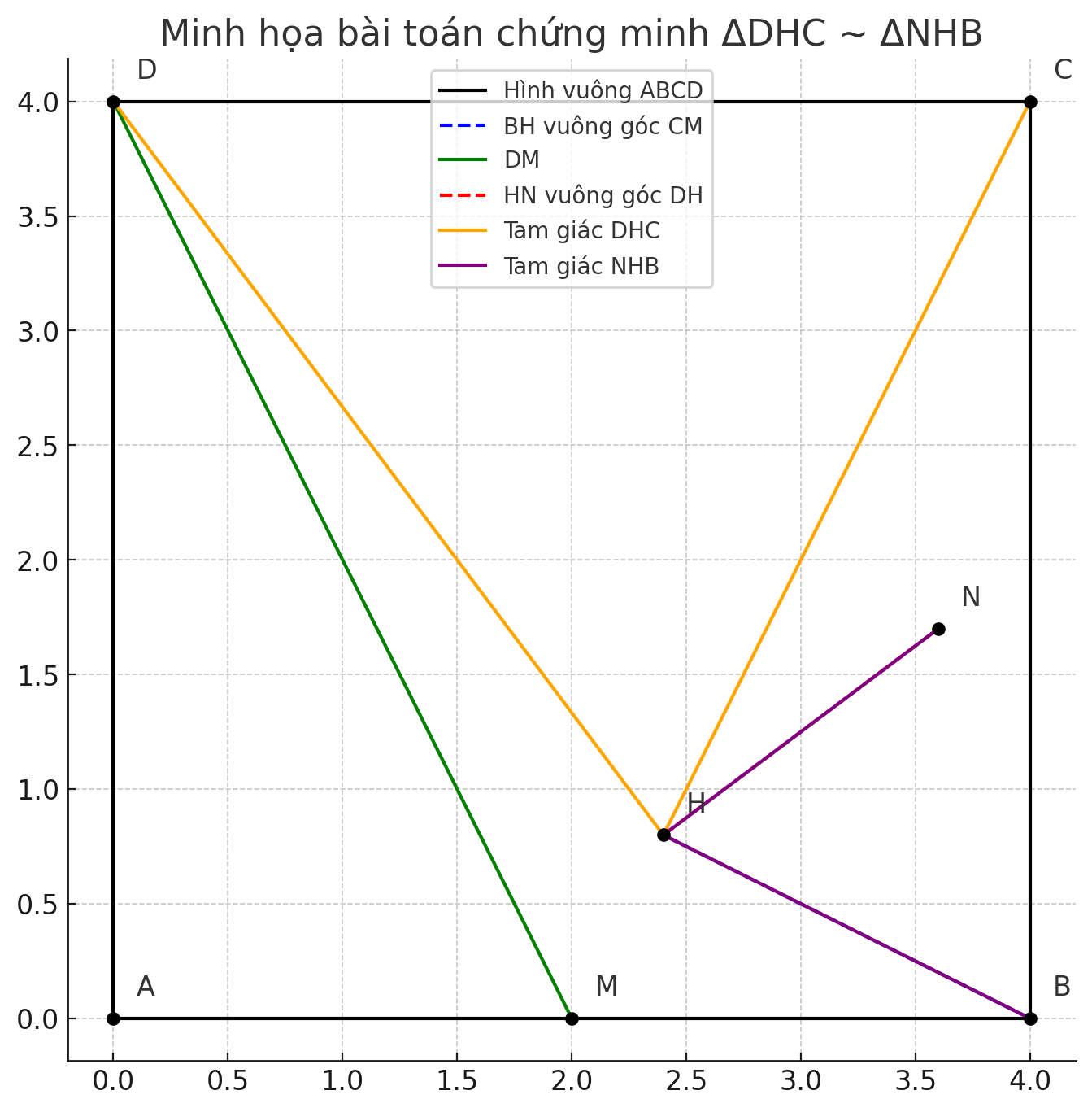
Xét hình vuông ABCD và các điểm M, H, N như mô tả.
Ta có:
Góc DHC = góc NHB = 90 độ (do BH vuông góc CM và HN vuông góc DH)
Góc HCD = góc HBN (cùng phụ với góc BCH)
=> tam giác DHC đồng dạng với tam giác NHB do có 2 góc tương ứng bằng nhau (g.g).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


