a) Chứng minh \( \Delta AHB \sim \Delta CAB \)

Xét 2 tam giác: \( \Delta AHB \) và \( \Delta CAB \)

- Cả hai tam giác đều có góc \( \angle B \) chung.
- \( \Delta ABC \) vuông tại A nên \( \angle CAB = 90^\circ \), mà \( AH \perp BC \Rightarrow \angle AHB = 90^\circ \)

⟹ \( \angle AHB = \angle CAB = 90^\circ \)

⟹ 2 tam giác có 2 góc bằng nhau ⟹ đồng dạng theo g.g (góc – góc)

 Vậy:
\[
\Delta AHB \sim \Delta CAB
\]

b) Chứng minh: \( AH^2 = BH \cdot HC \)

Từ tam giác vuông \( \Delta ABC \), đường cao AH ứng với cạnh huyền BC, ta có hệ thức lượng trong tam giác vuông:

\[
AH^2 = BH \cdot HC
\]

 Đây là một hệ thức quen trong tam giác vuông có đường cao hạ từ đỉnh vuông góc với cạnh huyền.

 Vậy đpcm.

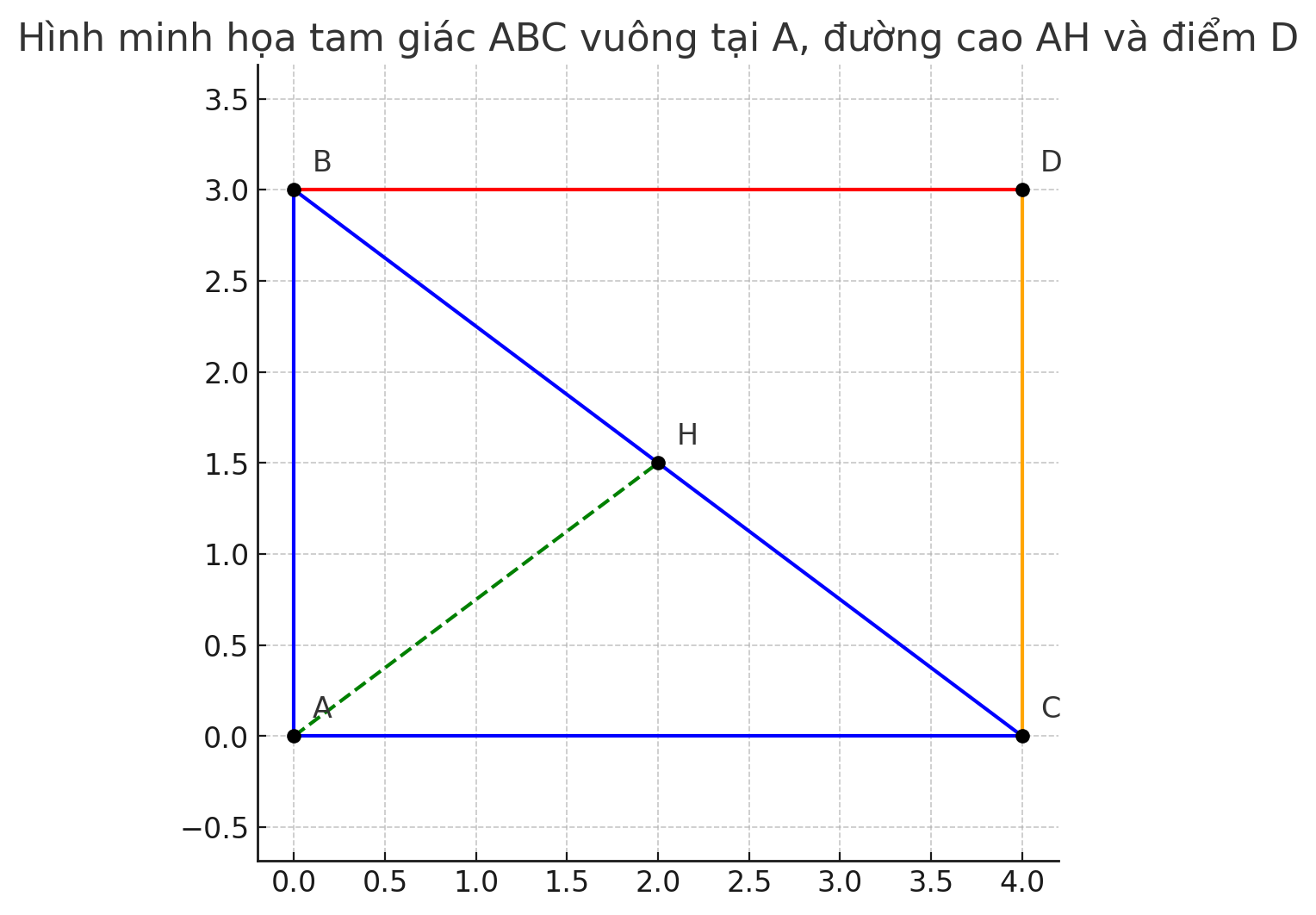
c) Qua B kẻ đường thẳng song song AC, cắt tia AH tại D. Tính diện tích tứ giác ABCD, biết AB = 3 cm, AC = 4 cm

- Qua B kẻ đường thẳng song song với AC, cắt tia AH tại D
→ Vì BD ∥ AC nên tứ giác ABCD là *ình thang vuông (vuông tại A và B)

Giờ ta chia tứ giác ABCD thành:
- tam giác ABC (vuông tại A)
- tam giác ABD (vuông tại B, vì BD ∥ AC mà AC ⟂ AB)

Tính diện tích \( S_{ABCD} = S_{ABC} + S_{ABD} \)**

Tam giác ABC vuông tại A, có AB = 3, AC = 4

\[
S_{ABC} = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 3 \cdot 4 = 6 \text{ cm}^2
\]

Vì BD ∥ AC và AC = 4 nên BD = 4 (do BD là đường song song với AC qua B, tam giác ABD là vuông tại B).
Mà AB = 3 là cạnh góc vuông còn lại.

\[
S_{ABD} = \frac{1}{2} \cdot AB \cdot BD = \frac{1}{2} \cdot 3 \cdot 4 = 6 \text{ cm}^2
\]

Tổng diện tích tứ giác ABCD:
\[
S_{ABCD} = S_{ABC} + S_{ABD} = 6 + 6 = \boxed{12 \text{ cm}^2}
\]