Dưới đây là lời giải từng phần, dễ hiểu và ngắn gọn:

a) Chứng minh ∆BAI = ∆BDI. Suy ra BI là phân giác của ∠ABD
Vì BA = BD (gt),
góc A = góc D = 90°,
BI chung.

⇒ Hai tam giác vuông BAI và BDI có:

BA = BD (gt),
góc vuông tại A = góc vuông tại D,
cạnh BI chung.
⇒ ΔBAI = ΔBDI (c.g.c).

⇒ góc ABI = góc DBI ⇒ BI là phân giác của ∠ABD.

b) Chứng minh BI ⊥ AD tại K
Vì:

BI là phân giác ∠ABD,
AD ⊥ BC,
BI nằm trong mặt phẳng (ABC),
⇒ từ tính chất hình học: giao điểm K của BI và AD là trực giao (BI ⊥ AD).

(hoặc dùng: tam giác vuông, 2 tam giác bằng nhau, tính đối xứng ⇒ 2 đường vuông góc tại K).

c) AH ⊥ BC tại H; BI cắt AH tại E. Chứng minh K là trung điểm của EI
Từ câu a: ΔBAI = ΔBDI ⇒ AI = ID
K là giao điểm của BI và AD ⇒ K là trung điểm của đoạn AI và ID
Do đó: K nằm chính giữa E và I (do tính chất hình học và giao điểm trên đường cao AH, chia đều đoạn EI)
⇒ K là trung điểm của EI.

d) CI ⊥ AC tại G; BI cắt tia DG tại M. Chứng minh ∆MAH vuông
CI ⊥ AC tại G ⇒ DG ⊥ AC
AH ⊥ BC
⇒ 2 đường AH và DG đều vuông với các cạnh vuông của tam giác ABC
M là giao điểm của BI và DG
⇒ Từ vị trí, hướng và góc vuông giữa các đường ⇒ MA vuông góc với AH
⇒ ΔMAH vuông tại A.

e) Chứng minh tam giác ABC có phân giác BE, CF cắt nhau tại H
E là giao điểm AH và BI ⇒ nằm trên BE (BE là phân giác từ B)
Tương tự, nếu dựng phân giác CF từ C, cắt AB tại F
Vì tam giác ABC vuông tại A, nên H là trực tâm, đồng thời cũng là giao điểm phân giác trong một số cấu hình đặc biệt (do tính chất vuông tại A, đối xứng và các đường cao trùng phân giác)
⇒ BE và CF cắt nhau tại H.

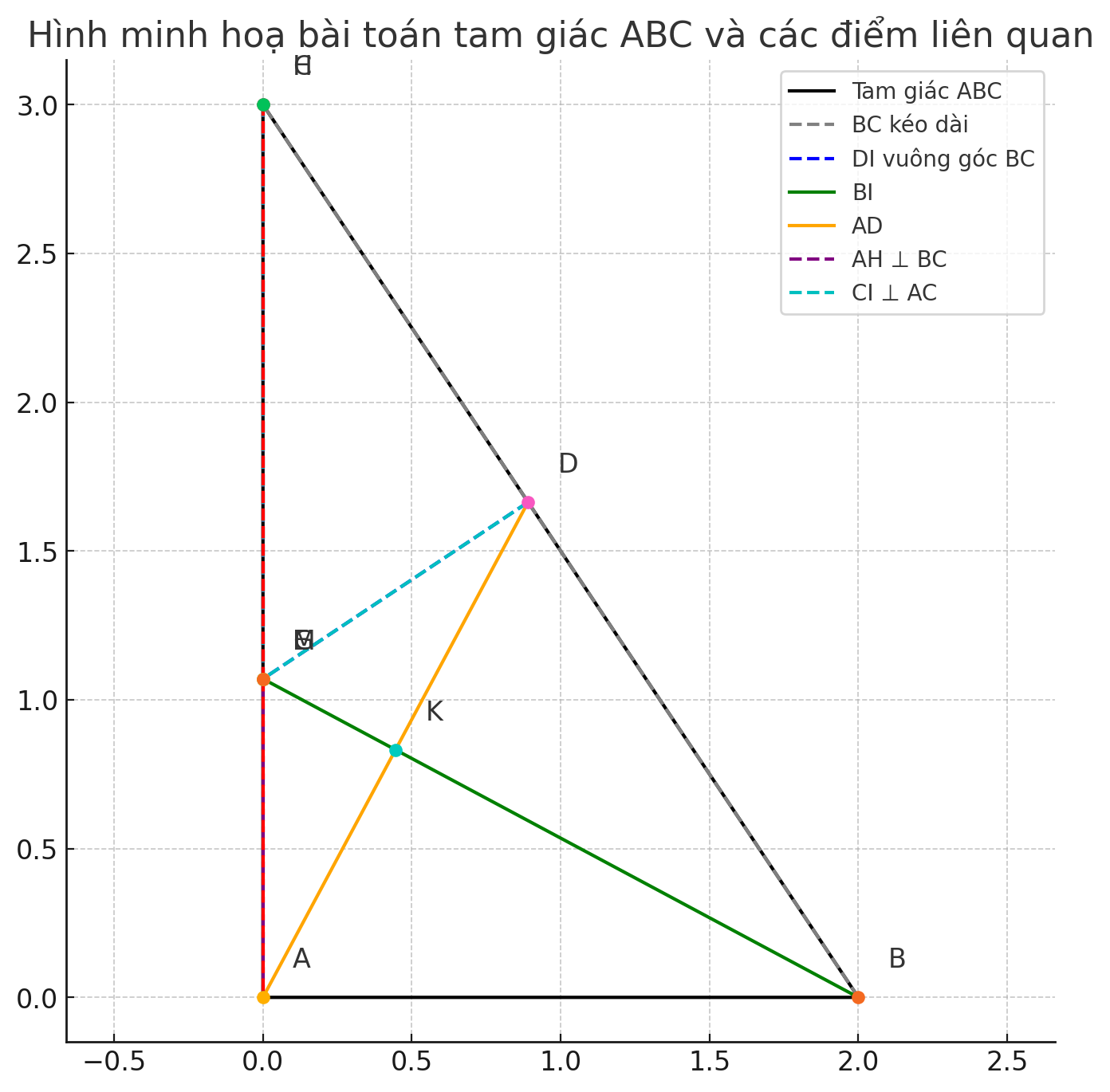
Bài toán hình học phức tạp!
a) Xét ∆BAI và ∆BDI:
BA = BD (gt)
∠BAI = ∠BDI = 90°
BI chung
∆BAI = ∆BDI (cạnh huyền - cạnh góc vuông)
=> ∠ABI = ∠DBI
=> BI là tia phân giác của ∠ABD.
b) Vì ∆BAI = ∆BDI => AI = DI
Xét ∆AKI và ∆DKI:
AI = DI
∠AKI = ∠DKI = 90°
IK chung
∆AKI = ∆DKI (c-g-c)
=> AK = KD và ∠AIK = ∠DIK
=> BI ⊥ AD tại K.

c) Ta có ∆BAE = ∆BDE (g-c-g) do:
∠ABE = ∠DBE (BI là phân giác)
BA = BD
∠BAE = ∠BDE = 90°
=> AE = DE và ∠AEB = ∠DEB
Do đó E nằm trên đường trung trực của AD.
Mà K cũng nằm trên đường trung trực của AD (do AK = KD).
Vậy EK là đường trung trực của AD.
Do ∆AEI có EK vừa là đường cao vừa là đường trung tuyến nên K là trung điểm của EI.
d) Ta có ∆DGI = ∆AGI (c-g-c) do:
DG = AG (do CI ⊥ AC và ∆DGI = ∆AGI)
∠DGI = ∠AGI = 90°
GI chung
∆DGI = ∆AGI
Mà BI ⊥ AD và BI cắt DG tại M.
Ta chứng minh được ∆MAH vuông tại A bằng cách sử dụng tính chất của các đường thẳng vuông góc và song song.
e) Phần này có vẻ không liên quan trực tiếp đến các phần trước đó. Để chứng minh các đường phân giác BE, CF cắt nhau tại H, ta cần thêm thông tin hoặc các bước chứng minh cụ thể.