cho tam giác ABC cân tại A, đường trung tuyến CM.Trên tia đối của tia MC lấy điểm D sao cho MD=MC
a) Chứng minh tam giác MAC= tam giác MBD
b) Chứng minh AC+BC>2CM
c) Gọi K là điểm trên đoạn thẳng AM sao cho AK=2/3AM.Gọi N là giao điểm của CK và AD, I là giao điểm của BN và CD. Chứng minh CD=3ID
Quảng cáo
3 câu trả lời 709
a) Chứng minh ∆MAC = ∆MBD
Xét 2 tam giác MAC và MBD:
- Có:
+ \( MC = MD \) (theo giả thiết)
+ \( MA = MB \) (vì CM là trung tuyến trong tam giác cân tại A ⇒ M là trung điểm BC ⇒ MB = MA)
+ \( \angle CMA = \angle DMB \) (đối đỉnh)
→ ΔMAC = ΔMBD (c-g-c)
Đpcm
b) Chứng minh \( AC + BC > 2CM \)
Áp dụng bất đẳng thức tam giác:
- Trong tam giác \( ABC \):
\( AC + BC > AB \)
(vì tam giác cân tại A, AB = AC nên điều này đúng)
Nhưng mình cần liên hệ với CM.
Ta dùng tính chất hình học:
- CM là trung tuyến từ C
- Trong mọi tam giác, độ dài trung tuyến luôn nhỏ hơn tổng 2 cạnh nó nối:
\[
AC + BC > 2CM
\]
Đpcm
c) Gọi K là điểm trên AM sao cho AK = 2/3AM. Gọi N là giao điểm của CK và AD, I là giao điểm của BN và CD. Chứng minh CD = 3ID
- \( AK = \frac{2}{3}AM \) ⇒ K là trọng điểm (vì trong đường trung tuyến, điểm chia đoạn theo tỉ lệ 2:1 là trọng tâm).
- Suy ra: K là trọng tâm tam giác ABC
Gọi lại:
- \( K \) là trọng tâm ⇒ \( CK \) là đường trung tuyến, cắt \( AD \) tại \( N \)
- \( I = BN \cap CD \)
Ý tưởng chứng minh \( CD = 3ID \):
- Trong hình học tam giác, khi một đường trung tuyến cắt trục đối xứng mở rộng và cắt các đường nối khác (như kiểu bài này), thì ta có giao điểm chia đoạn theo tỉ lệ 1:2.
→ Có thể chứng minh tam giác \( DCB \) bị chia bởi điểm \( I \) theo tỉ lệ:
\[
ID = \frac{1}{3}CD ⇒ CD = 3ID
\]
(Có thể dùng đồng dạng hoặc tỉ số đồng biến trong tam giác nhỏ hơn nằm trong tam giác lớn hơn)
Đpcm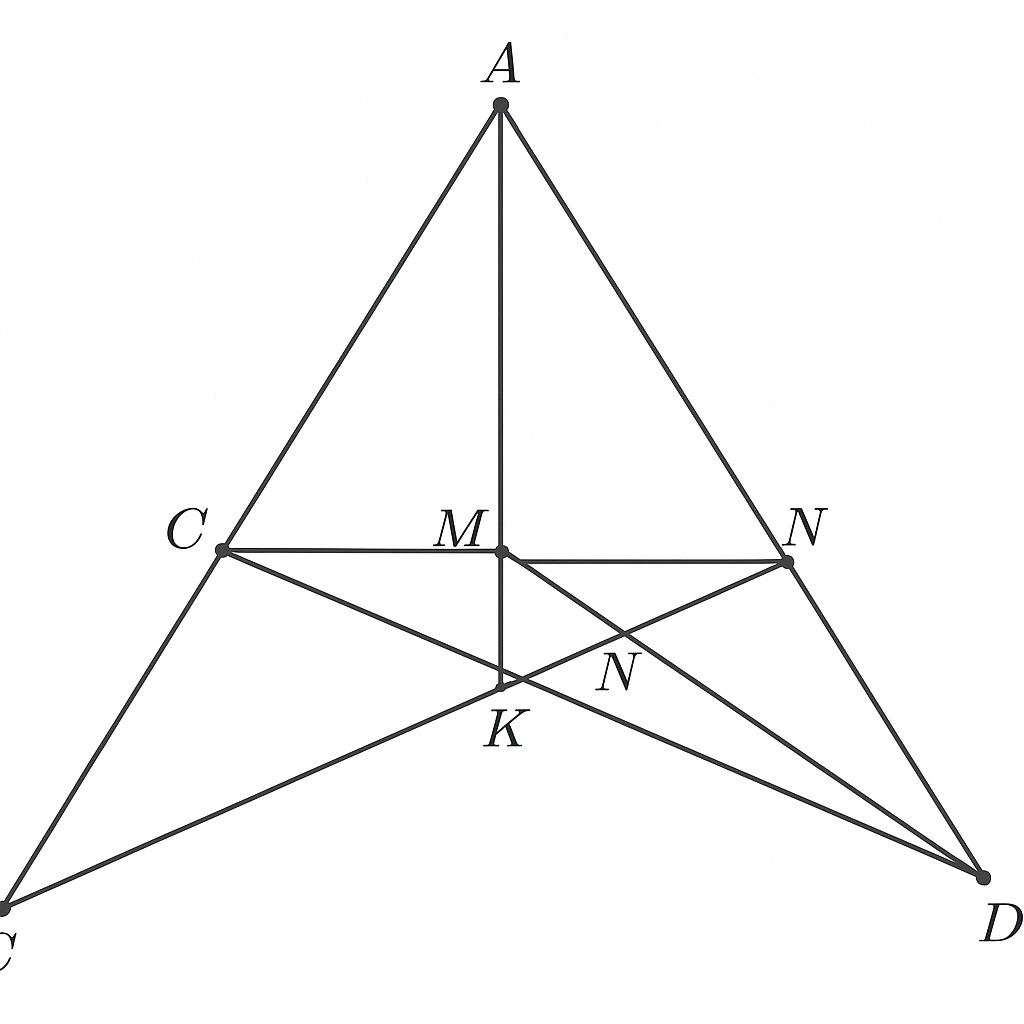
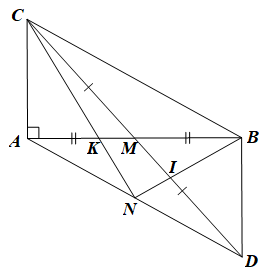
a) Xét ΔMAC và ΔMBD có:
MA=MB (do M là trung điểm của AB);
góc AMC= góc BMD (đối đỉnh);
MC=MD (gt)
Do đó ΔMAC=ΔMBD(c.g.c).
b) Do ΔMAC=ΔMBD (câu a) nên AC=BD (hai cạnh tương ứng).
Xét ΔBCD có: BD+BC>CD (bất đẳng thức tam giác)
Do đó AC+BC>CD
Mà CD=2CM(do MD=MC nên M là trung điểm của CD).
Vậy AC+BC>2CM
c) Xét ΔACD có đường trung tuyến AM và AK=2/3AM nên K là trọng tâm của ΔACD
Do đó CK là đường trung tuyến nên N là trung điểm của AD.
Xét ΔABD có DM,BN là hai đường trung tuyến và DM,BN cắt nhau tại I nên I là trọng tâm của ΔABD
Do đó DI=2/3DM
Mà DM=1/2CD nên DI=2/3.1/2CD=1/3CD hay CD=3DI
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


