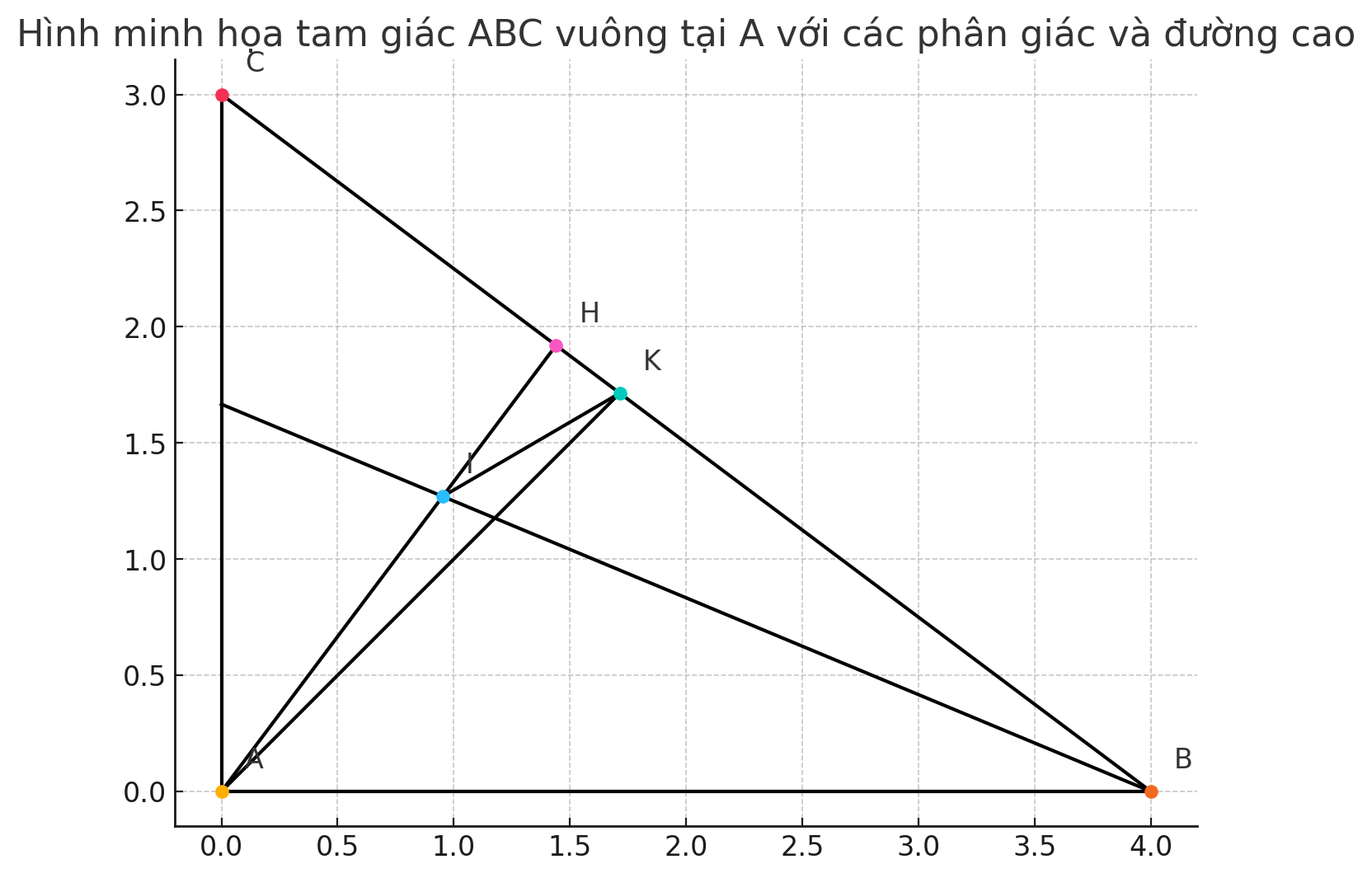
Cho tam giác ABC vuông tại A , đường cao AH
a. Chứng minh tam giác ABC đòng dạng với tam giác HBA . Từ đó suy ra AB.HA = HB.AC
b. Tia phân giác của góc ABC cắt AH tại I . Tia phân giác góc HAC cắt BC tại K . C hứng minh IH.KC = IA.KH
c. Chứng minh IK // AC
Giúp mình với ạ
Quảng cáo
1 câu trả lời 703
a) Chứng minh tam giác ABC ∼ HBA
Xét hai tam giác: ABC và HBA
- Tam giác ABC vuông tại A (gt)
- Tam giác HBA cũng vuông tại H, vì AH ⊥ BC
- Góc chung: ∠B
⇒ Tam giác ABC và HBA có:
- Một góc vuông
- Một góc B chung
→ Hai tam giác đồng dạng theo trường hợp góc – góc (g.g)
Suy ra hệ thức:
Từ tam giác ABC ∼ HBA, ta có tỉ lệ:
\[
\frac{AB}{HB} = \frac{AC}{AB}
\Rightarrow AB^2 = HB \cdot AC
\Rightarrow \boxed{AB \cdot HA = HB \cdot AC}
\]
Đẳng thức cần chứng minh được suy ra từ đồng dạng.
b) Gọi I là giao điểm của phân giác ∠ABC với AH, K là giao điểm phân giác ∠HAC với BC
Chứng minh: \( \boxed{IH \cdot KC = IA \cdot KH} \)
- Sử dụng tính chất đường phân giác và đồng dạng tam giác
- Kết hợp hệ thức tỉ số cạnh – đoạn phân giác
Xét tam giác BHC có tia phân giác AI (giao AH tại I)
Do I nằm trên AH và AI là tia phân giác góc B, ta dùng tính chất phân giác trong tam giác vuông:
Từ các tam giác nhỏ được tạo thành:
- Xét các tam giác đồng dạng:
- Tam giác IHC ∼ IAK (do có góc đối đỉnh và cùng chung góc phân giác)
⇒ Theo đồng dạng:
\[
\frac{IH}{IA} = \frac{KH}{KC}
\Rightarrow IH \cdot KC = IA \cdot KH
\]
c) Chứng minh IK // AC
- Dùng tính chất đồng dạng tam giác hoặc tỉ số đồng biến
- Hoặc dùng hệ thức hình học từ đồng dạng
Từ câu b) ta có:
- \( \frac{IH}{IA} = \frac{KH}{KC} \)
Xét các tam giác:
- Tam giác IAK và HKC
- Có: \( \frac{IA}{IH} = \frac{KC}{KH} \)
- Có góc chung tại K
→ ⇒ Hai tam giác đồng dạng
→ Đồng dạng ⇒ IK // AC
\( \boxed{IK \parallel AC} \)
- a) Tam giác ABC ∼ HBA ⇒ AB·HA = HB·AC
- b) IH·KC = IA·KH
- c) IK // AC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6297
Đã trả lời bởi chuyên gia
6297 -
 Đã trả lời bởi chuyên gia
4613
Đã trả lời bởi chuyên gia
4613 -
 Đã trả lời bởi chuyên gia
4106
Đã trả lời bởi chuyên gia
4106 -
 Đã trả lời bởi chuyên gia
4056
Đã trả lời bởi chuyên gia
4056


