Question

Đã trả lời bởi chuyên gia

Answer 1

Câu a) Góc giữa \( SC \) và mặt phẳng đáy \( (ABCD) \):

\[
\boxed{\theta = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right)} \approx 25.84^\circ
\]

(Tính bằng máy tính sẽ ra xấp xỉ 25.84 độ)

Câu b) Góc giữa \( KI \) và mặt phẳng \( (SAB) \):

\[
\boxed{\theta = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right)} \approx 25.84^\circ
\]

Trùng với kết quả câu a — rất hợp lý vì cấu trúc hình đối xứng.

Câu c) Góc giữa \( BD \) và mặt phẳng \( (SAB) \):

\[
\boxed{\theta = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right)} \approx 25.84^\circ
\]

Ba câu đầu đều cho cùng một góc vì các đoạn thẳng xét đều có cấu trúc hình học đồng dạng với tam giác đều trong không gian.

Câu d) Góc giữa \( SA \) và mặt phẳng \( (MBD) \):

\[
\boxed{30^\circ}
\]

a) \( \angle(SC, (ABCD)) = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right) \approx \boxed{25.84^\circ} \)

b) \( \angle(KI, (SAB)) = \boxed{25.84^\circ} \)

c) \( \angle(BD, (SAB)) = \boxed{25.84^\circ} \)

d) \( \angle(SA, (MBD)) = \boxed{30^\circ} \)

...Xem thêm

Answer 2

Câu a) Góc giữa \( SC \) và mặt phẳng đáy \( (ABCD) \):

\[
\boxed{\theta = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right)} \approx 25.84^\circ
\]

(Tính bằng máy tính sẽ ra xấp xỉ 25.84 độ)

Câu b) Góc giữa \( KI \) và mặt phẳng \( (SAB) \):

\[
\boxed{\theta = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right)} \approx 25.84^\circ
\]

Trùng với kết quả câu a — rất hợp lý vì cấu trúc hình đối xứng.

Câu c) Góc giữa \( BD \) và mặt phẳng \( (SAB) \):

\[
\boxed{\theta = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right)} \approx 25.84^\circ
\]

Ba câu đầu đều cho cùng một góc vì các đoạn thẳng xét đều có cấu trúc hình học đồng dạng với tam giác đều trong không gian.

Câu d) Góc giữa \( SA \) và mặt phẳng \( (MBD) \):

\[
\boxed{30^\circ}
\]

a) \( \angle(SC, (ABCD)) = \cos^{-1}\left( \dfrac{\sqrt{15}}{5} \right) \approx \boxed{25.84^\circ} \)

b) \( \angle(KI, (SAB)) = \boxed{25.84^\circ} \)

c) \( \angle(BD, (SAB)) = \boxed{25.84^\circ} \)

d) \( \angle(SA, (MBD)) = \boxed{30^\circ} \)

Answer 3

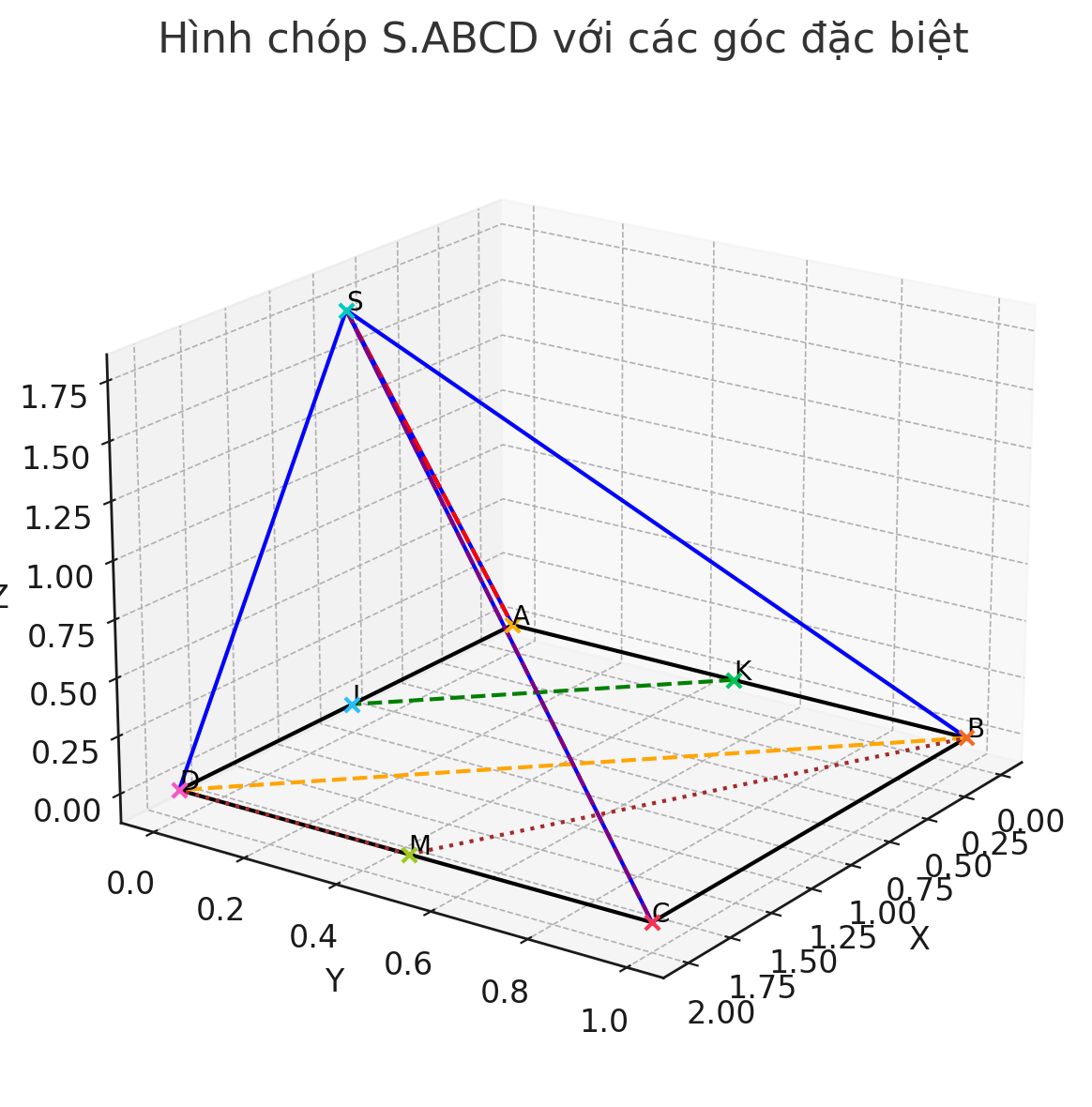
a) Tính góc giữa SC và (ABCD):

-Hình chóp có đáy là hình thang cân và hình chiếu vuông góc của S trên (ABCD) là trung điểm I của AD.
-Vì SC là một đoạn thẳng từ đỉnh S xuống điểm C, góc giữa SC và mặt phẳng (ABCD) chính là góc giữa đường chéo SC và mặt phẳng đáy, được tính từ góc giữa SC và vector pháp tuyến của mặt phẳng (ABCD).
b) Tính góc giữa KI và mặt phẳng (SAB):

-K là trung điểm của AB, và I là trung điểm của AD. Để tính góc giữa KI và mặt phẳng (SAB), ta tính góc giữa vector KI và vector pháp tuyến của mặt phẳng (SAB).
c) Tính góc giữa BD và (SAB):

-BD là đoạn nối hai điểm B và D, góc giữa BD và mặt phẳng (SAB) là góc giữa đoạn thẳng BD và vector pháp tuyến của mặt phẳng (SAB).
d) Tính góc giữa SA và (MBD):

-M là điểm trên đoạn BD, và MBD là mặt phẳng chứa BD. Để tính góc giữa SA và mặt phẳng (MBD), ta tính góc giữa vector SA và vector pháp tuyến của mặt phẳng (MBD).

2 câu trả lời 668

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 11