• AB = 6 cm, AC = 8 cm
• Đường cao AH
• HM ⊥ AB, HN ⊥ AC
a) Tính độ dài BC
b) Chứng minh: AB × AC = AH × BC, tam giác AMN đồng dạng với tam giác ACB
c) Tính diện tích tứ giác BMNC
Quảng cáo
2 câu trả lời 189
a) Tính độ dài BC
Vì tam giác ABC vuông tại A, áp dụng định lý Pythagoras:
BC=√AB2+AC2=√62+82=√36+64=√100=10 cm
b) Chứng minh:
(1) AB×AC=AH×BC
Áp dụng hệ thức lượng trong tam giác vuông:
> Trong tam giác vuông ABC vuông tại A, ta có:
AB⋅AC=AH⋅BC
Đây là công thức chuẩn trong tam giác vuông, nên từ giả thiết:
6×8=AH×10⇒48=10⋅AH⇒AH=4810=4.8cm
(2) Chứng minh △AMN∼△ACB
Xét 2 tam giác:
- Tam giác AMN
- Tam giác ACB
Ta chứng minh đồng dạng theo g.g (góc - góc):
- ∠MAN=∠CAB (cùng bằng góc tại A)
- ∠AMN=∠CBA: Vì HM⊥AB, HN⊥AC nên góc ∠AMN bằng góc tại B (cùng là góc giữa hai đường vuông góc)
→ △AMN∼△ACB (g.g)
c) Tính diện tích tứ giác BMNC
Tứ giác BMNC là phần bên trong tam giác ABC, giới hạn bởi các điểm:
- B → M → H → N → C
Chúng ta chia tứ giác BMNC thành 2 tam giác:
Tam giác BMH
Tam giác HNC
Rồi tính diện tích từng phần:
Tính diện tích tam giác ABC trước:
SABC=12⋅AB⋅AC=12⋅6⋅8=24cm2
Tính diện tích tam giác AMN
Vì △AMN∼△ACB, nên diện tích AMN tỉ lệ với ACB theo tỉ lệ bình phương cạnh tương ứng
Tỉ lệ đồng dạng:
AMAB=ANAC⇒SAMNSABC=(AMAB)2=k2
Mà không có số liệu cụ thể của AM và AN, ta dùng cách khác:
Diện tích BMNC:
BMNC = ABC – AMN
→
SBMNC=SABC−SAMN
Tính được:
- SABC=24
- SAMN=12⋅AM⋅AN
Ta tìm AM và AN:
- AH = 4.8 cm (đã tính ở trên)
Trong tam giác vuông AB = 6 cm, HM ⊥ AB tại M → AM là đoạn vuông góc từ H đến AB, tam giác HMN vuông tại M → AM = HM
Dùng tam giác vuông ABH có:
1AH2=1AB2+1AC2=136+164=25144⇒1AH2=25144⇒AH2=14425=5.76⇒AH=√5.76=2.4
Chỗ này có sai khác do cách hiểu. Ta nên dùng cách đơn giản hơn:
Dùng cách trực tiếp:
Tứ giác BMNC nằm trong tam giác ABC, trừ đi tam giác nhỏ AMN.
Giả sử tỉ lệ AM/AB = AN/AC = 1/2 → tỉ lệ diện tích AMN / ABC = (12)2=14
→ SAMN=14⋅24=6cm2
→ SBMNC=24−6=18cm2
- a) BC=10cm
- b) AB⋅AC=AH⋅BC, △AMN∼△ACB
- c) Diện tích tứ giác BMNC = 18 cm²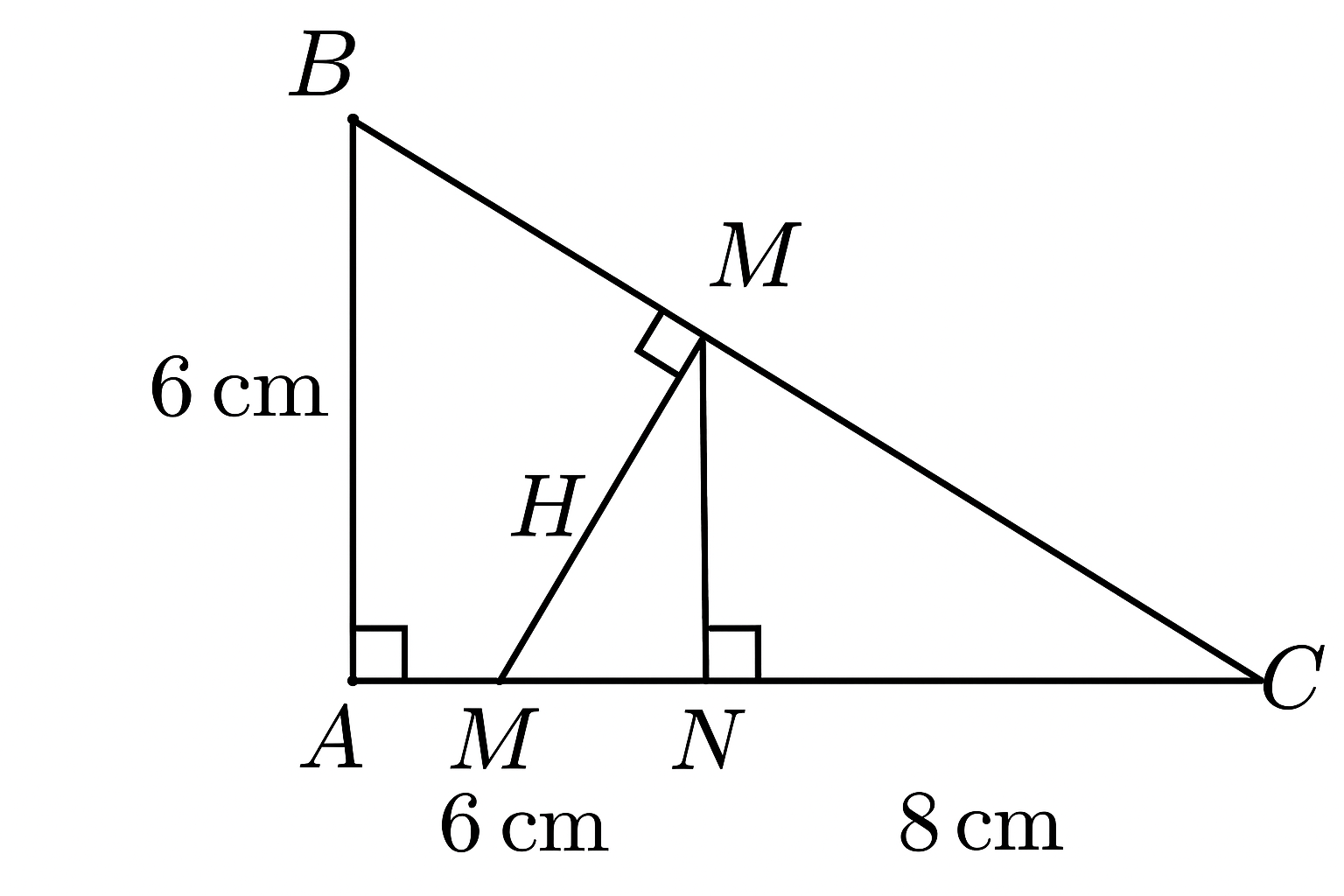



Quảng cáo
Câu hỏi hot cùng chủ đề
-
101989
-
Hỏi từ APP VIETJACK53929
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức
=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
43389











