Bài 3. Tam giác ABC có AB<AC. Trên cạnh AB lấy điểm M (M khác B).Trên nửa mặt...

· 14:38 05/04/2025

Bài 3. Tam giác ABC có AB<AC. Trên cạnh AB lấy điểm M (M khác B).Trên nửa mặt phẳng bờ AB không chứa C vẽ tia Mx song song AC và trên tia này lấy điểm N sao cho MN = MB.Chứng minh rằng BC<NC

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

2 câu trả lời 148

Sang Phạm

4 tháng trước

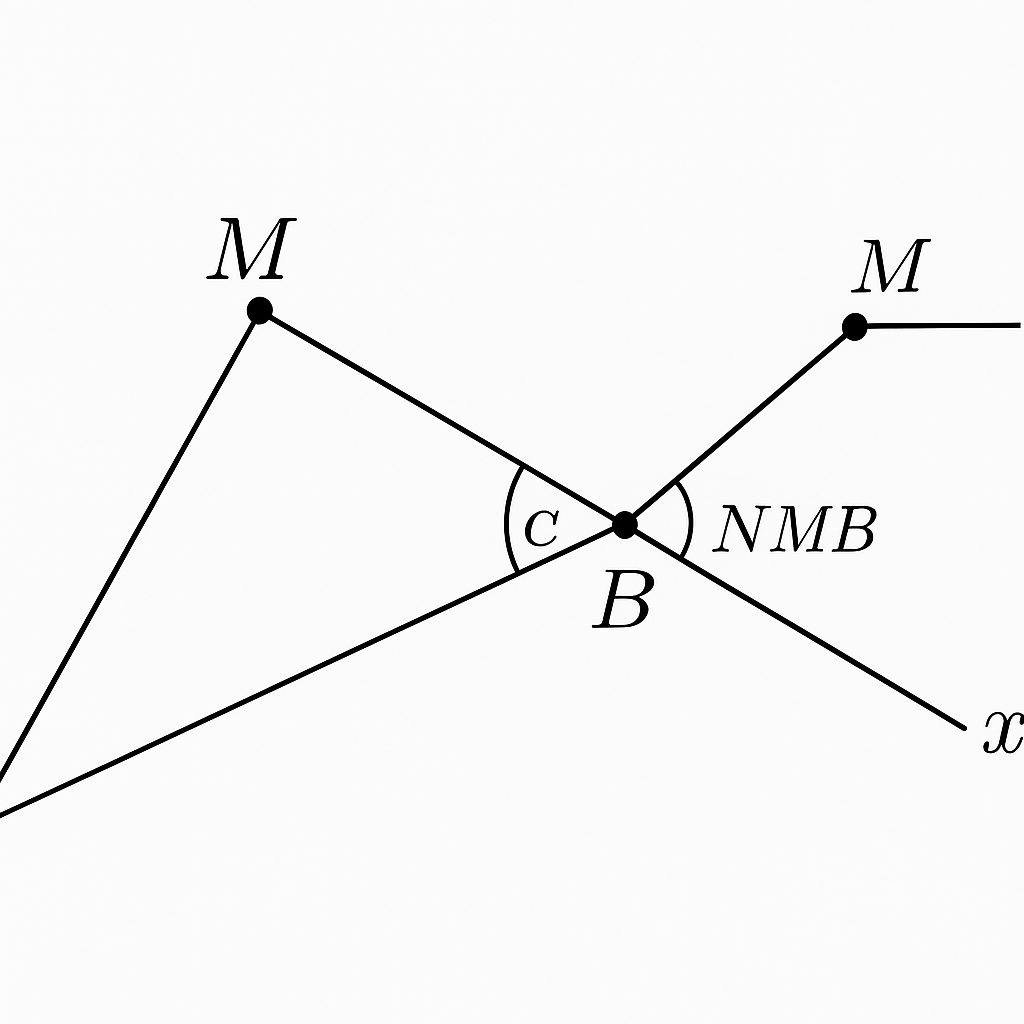
Ta có: $MN = MB$ ⇒ Tam giác $MNB$ là tam giác cân tại M
- Do $Mx \parallel AC$ , suy ra:
$\angle NMB = \angle ACB \quad \text{(vì là cặp góc so le trong)}$

Dựa vào tam giác cân $MNB$

- Tam giác $MNB$ cân tại $M$ , nên:
$\angle NBM = \angle NMB$
- Ta vừa có: $\angle NMB = \angle ACB$

⇒ Suy ra:
$\angle NBM = \angle ACB \tag{1}$

So sánh góc $\angle CBM$ và $\angle NBM$

- Xét tam giác $ABC$ với $AB < AC$ ⇒ cạnh đối diện góc nhỏ hơn ⇒
$\angle ABC < \angle ACB \tag{2}$

- Từ (1) và (2) ⇒
$\angle CBM < \angle NBM$

Cùng xét trong tam giác $CBM$ và $NBM$

Cùng có cạnh $BM$ , và cùng kéo đến điểm $C$ và $N$ theo 2 góc khác nhau (với $\angle NBM > \angle CBM$ )

→ Góc lớn đối diện cạnh lớn ⇒
$\boxed{BC < NC}$

$\boxed{BC < NC}$

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Ngọc

4 tháng trước

Sử dụng giả thiết AB < AC:

∠ACB < ∠ABC. (1)

giả thiết MN = MB:

∠MBN = ∠MNB. (2)

giả thiết Mx || AC:

Vì tia Mx song song với AC (Mx chứa đoạn MN), nên MN || AC.

Xét hai đường thẳng song song MN và AC bị cắt bởi đường thẳng NC

Khi đó, hai góc so le trong bằng nhau:

∠MNC = ∠ACN.

Vì A, C, N là các đỉnh tam giác hoặc các điểm xác định, góc ∠ACN chính là góc ∠ACB của tam giác ABC.

Do đó: ∠MNC = ∠ACB. (3)

Xét góc ∠BNC: Góc này được tạo thành từ hai góc kề nhau là ∠BNM và ∠MNC. ∠BNC = ∠BNM + ∠MNC. Thay (2) và (3) vào, ta có: ∠BNC = ∠MBN + ∠ACB. (4)

Xét góc ∠NBC: Góc này là góc tại đỉnh B của tam giác BNC. Điểm N nằm trên nửa mặt phẳng bờ AB không chứa C, nghĩa là N và C nằm về hai phía khác nhau so với đường thẳng AB. Do đó, tia BN nằm "ngoài" góc ∠ABC (so với tia BA). Vì vậy, góc ∠NBC được tạo thành bằng cách cộng góc ∠ABC và góc ∠NBA (hay ∠MBN): ∠NBC = ∠ABC + ∠NBA = ∠ABC + ∠MBN. (5)

hai góc của tam giác BNC:

Chúng ta cần chứng minh BC < NC. Trong tam giác BNC, điều này tương đương với việc chứng minh góc đối diện với cạnh BC nhỏ hơn góc đối diện với cạnh NC. Tức là, ta cần chứng minh:

∠BNC < ∠NBC.

Sử dụng biểu thức (4) và (5), bất đẳng thức trên trở thành: ∠MBN + ∠ACB < ∠ABC + ∠MBN.

Trừ ∠MBN ở cả hai vế, ta được: ∠ACB < ∠ABC.

Bất đẳng thức ∠ACB < ∠ABC chính là kết quả chúng ta có được từ giả thiết AB < AC ở bước 1.

Vì ∠ACB < ∠ABC đúng, nên bất đẳng thức ∠BNC < ∠NBC

Trong tam giác BNC, vì góc ∠BNC < ∠NBC, nên cạnh đối diện với góc ∠BNC (là cạnh BC) phải nhỏ hơn cạnh đối diện với góc ∠NBC (là cạnh NC).

Vậy, BC < NC. (dpcm)

...Xem thêm

(+1) 1 bình luận

leanh · 4 tháng trước

bạn ơi vẽ hình cho mình với

Đăng nhập để hỏi chi tiết

Quảng cáo

2 câu trả lời 148

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 7