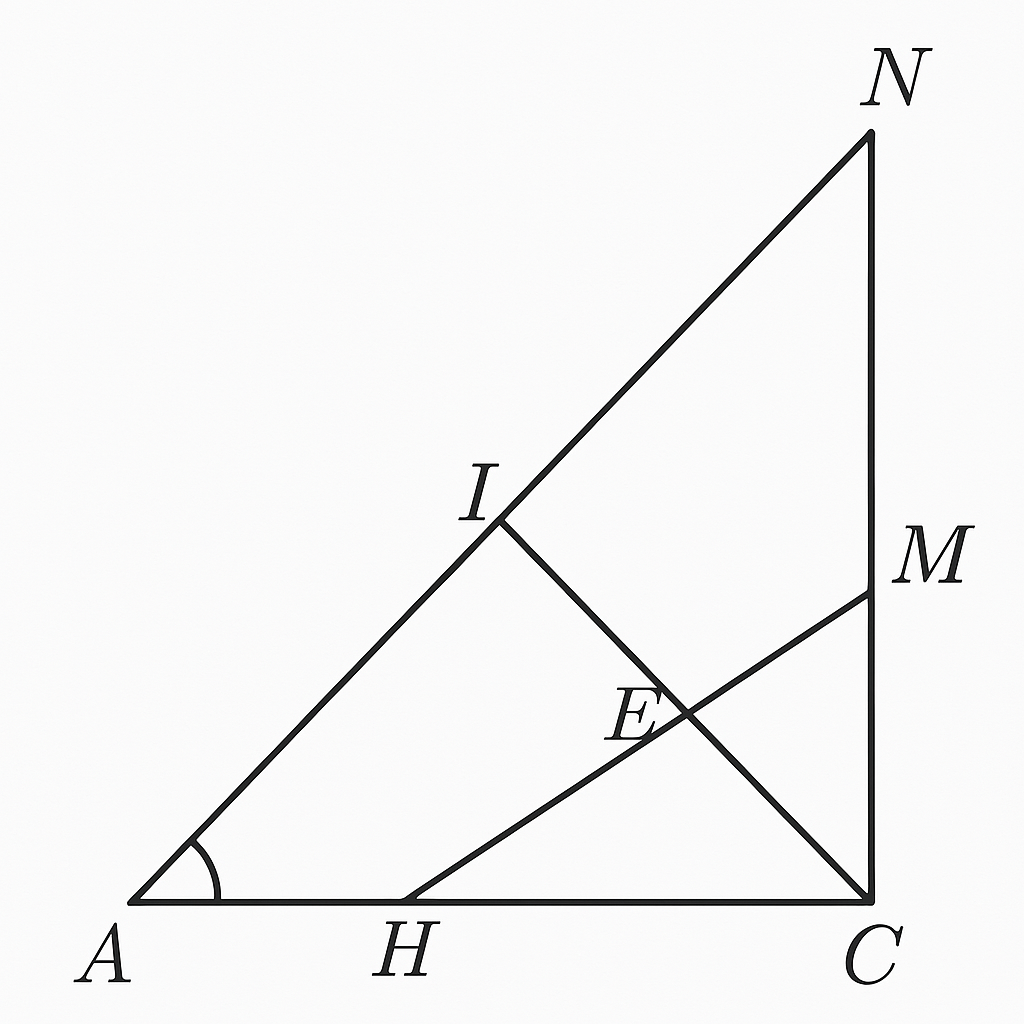
Cho ΔABC vuông tại A ( AB &lt; AC), đường cao AH, lấy điểm I trên cạnh BC sao ch...

· 10:10 05/04/2025

Cho ΔABC vuông tại A ( AB < AC), đường cao AH, lấy điểm I trên cạnh BC sao cho H là trung điểm của BI, đường thẳng đi qua C vuông góc với tia AI tại M cắt tia AH tại N.

a) CM: ΔAIH đồng dạng với ΔCIM

b) Khi BC = 10cm, AC = 8cm, tính độ dài đoạn thẳng

CH.

c) Gọi E là giao điểm của NI và AC. CM: NE.NI = AN.HN

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

2 câu trả lời 276

Sang Phạm

8 tháng trước

a) Chứng minh \( \Delta AIH \sim \Delta CIM \)

Xét hai tam giác \( AIH \) và \( CIM \):

- \( \angle AIH = \angle CIM \) (do cùng vuông vì \( AH \perp BC \), và \( CM \perp AI \))
- Hai tam giác có góc chung là \( \angle I \)

→ Hai tam giác có hai góc bằng nhau ⇒ đồng dạng (g.g)

\[
\boxed{\Delta AIH \sim \Delta CIM}
\]

b) Cho \( BC = 10\, \text{cm},\ AC = 8\, \text{cm} \). Tính độ dài \( CH \)

Tam giác vuông tại A → dùng hệ thức lượng:

- \( \Delta ABC \) vuông tại A ⇒ \( AB^2 + AC^2 = BC^2 \)
\[
AB^2 + 8^2 = 10^2 \Rightarrow AB^2 = 100 - 64 = 36 \Rightarrow AB = 6\, \text{cm}
\]

- \( AH \) là đường cao từ A trong tam giác vuông ABC ⇒ áp dụng công thức:
\[
AH = \frac{AB \cdot AC}{BC} = \frac{6 \cdot 8}{10} = \frac{48}{10} = 4.8\, \text{cm}
\]

- Tính \( CH \): ta dùng hệ thức lượng trong tam giác vuông:
\[
CH = \frac{AC^2}{BC} = \frac{8^2}{10} = \frac{64}{10} = \boxed{6.4\, \text{cm}}
\]

c) Gọi \( E \) là giao điểm của \( NI \) và \( AC \). Chứng minh: \( NE \cdot NI = AN \cdot HN \)

Dùng đồng dạng \( \Delta AIH \sim \Delta CIM \):

\[
\Rightarrow \frac{AI}{CI} = \frac{AH}{CM} = \frac{IH}{IM}
\]

Xét hai tam giác đồng dạng và tam giác vuông nhỏ \( \Delta ANI \sim \Delta ENI \)

- Góc \( ANH = ENI \) (đối đỉnh)
- \( \angle ANH = \angle EIN = 90^\circ \)

→ Tam giác đồng dạng \( \Delta ANI \sim \Delta ENI \) ⇒ theo hệ thức:
\[
NE \cdot NI = AN \cdot HN
\]

\[
\boxed{NE \cdot NI = AN \cdot HN}
\]

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Ngọc

8 tháng trước

Xét ΔABH và ΔAHI:

AH là cạnh chung.

∠AHB = ∠AHI = 90° (Vì AH ⊥ BC).

BH = HI (Theo giả thiết H là trung điểm BI).

=> ΔABH ≅ ΔAHI

=> AB = AI (Hai cạnh tương ứng).

=> ΔABI là tam giác cân tại A.

Trong tam giác cân ABI, đường cao AH cũng là đường phân giác của ∠BAI. => ∠BAH = ∠HAI.
CM

∠HAI = ∠MCI:

Trong ΔABC vuông tại A, ta có ∠BAH + ∠ABH = 90°.

Trong ΔABC vuông tại A, ta có ∠ACB + ∠ABH = 90°.

=> ∠BAH = ∠ACB (hay ∠MCI).

Mà ∠BAH = ∠HAI (chứng minh trên).

=> ∠HAI = ∠MCI (hay ∠ICH).

Xét ΔAIH và ΔCIM:

∠AHI = 90° (AH ⊥ BC).

∠CMI = 90° (CM ⊥ AI theo giả thiết).

=> ∠AHI = ∠CMI = 90°.

∠HAI = ∠MCI (chứng minh trên).

=> ΔAIH ~ ΔCIM (g.g - góc.góc).
B/

Xét ΔABC vuông tại A, đường cao AH.

Áp dụng hệ thức lượng trong tam giác vuông TA CÓ

Thay số: 8² = CH * 10 64 = CH * 10 CH = 64 / 10 = 6.4 cm.
c/

Chứng minh AI ⊥ NI (∠AIN = 90°):

∠HAI = ∠BAH và ∠BAH = ∠BCA (∠C).( cm phần a )

=> ∠HAI = ∠C.

Xét ΔAMN vuông tại M (do CM ⊥ AI tại M, N thuộc CM): ∠ANM + ∠NAM = 90° Vì N thuộc tia AH và M thuộc AI, nên ∠ANM = ∠ANI và ∠NAM = ∠NAI = ∠HAI. => ∠ANI + ∠HAI = 90°.

Thay ∠HAI = ∠C vào: ∠ANI + ∠C = 90°.

Xét ΔNAI: Tổng các góc trong tam giác bằng 180°. ∠NIA + ∠NAI + ∠ANI = 180° ∠NIA + ∠HAI + ∠ANI = 180° ∠NIA + ∠C + (90° - ∠C) = 180° (Thay ∠ANI = 90° - ∠C và ∠HAI = ∠C) ∠NIA + 90° = 180° ∠NIA = 90°.

Vậy, AI ⊥ NI tại I

Chứng minh ΔNEH ~ ΔNAI:

Xét ΔNEH và ΔNAI:

∠N (hay ∠ENH = ∠ANI) là góc chung.

∠NHE = 90° (Vì N thuộc đường thẳng AH, H thuộc BC và AH ⊥ BC).

∠NIA = 90° (Chứng minh trên).

=> ∠NHE = ∠NIA = 90°.

=> ΔNEH ~ ΔNAI (g.g - góc.góc).

Suy ra tỉ lệ và đẳng thức cần chứng minh:

Từ ΔNEH ~ ΔNAI, ta có tỉ lệ các cạnh tương ứng: NE / NA = NH / NI = EH / AI

Từ tỉ lệ NE / NA = NH / NI, nhân chéo ta được: NE * NI = NA * NH (hay NE * NI = AN * HN).