Bài 7. Cho tam giác ABC, đường trung tuyến AM . Gọi D là trung điểm của AM, E là giao điểm của BD và AC,F là trung điểm của EC . Biết AC = 9 cm, hỏi độ dài của đoạn thẳng AE bằng bao nhiêu
Bài 9. Cho A4BC vuông tại A có AB=8 cm, AC = 6 cm . Có M,N là trung điểm của AB, AC .
a) Vẽ phân giác AD với DeBC. Tính độ dài BD.
b) Chứng minh rằng BD.AN = AM.DC.
Bài 10. Cho 4ABC vuông tại A có AB<AC . Vẽ AH – BC tại H .
a) Chứng minh AHBA AABC.
b) Tính độ dài các cạnh BC và AH nếu AB=9 cm, AC =12cm.
c) Trên HC lấy điểm M sao cho HM = HA. Qua M vẽ đường thẳng vuông góc với BC cắt AC tại I. Qua C vẽ đường thẳng vuông góc với BC cắt tia phân giác IMC tại K. Chứng minh H,I,K thẳng
hàng.
Quảng cáo
2 câu trả lời 402
Bài 9
a) Vẽ phân giác AD, D thuộc BC. Tính độ dài BD.
Áp dụng định lý phân giác trong tam giác ABC:
\[
\frac{BD}{DC} = \frac{AB}{AC} = \frac{8}{6} = \frac{4}{3}
\]
Tính độ dài BC:
\[
BC = \sqrt{AB^2 + AC^2} = \sqrt{64 + 36} = \sqrt{100} = 10 \text{ cm}
\]
Gọi BD = x → DC = 10 - x
\[
\frac{x}{10 - x} = \frac{4}{3} \Rightarrow 3x = 40 - 4x \Rightarrow 7x = 40 \Rightarrow x = \frac{40}{7} \approx 5,71 \text{ cm}
\]
BD = 40/7 cm
b) Chứng minh BD · AN = AM · DC
Ta có:
- AN là trung tuyến ⇒ AN nối A với trung điểm N của AC
- AM nối A với trung điểm M của AB
=> AM và AN là trung tuyến
Từ bài toán đã có BD = 40/7 và DC = 30/7
- AN = 3 cm
- AM = 4 cm
Thử nhân:
- BD · AN = (40/7) · 3 = 120/7
- AM · DC = 4 · (30/7) = 120/7
=> Hai vế bằng nhau
⇒ Đpcm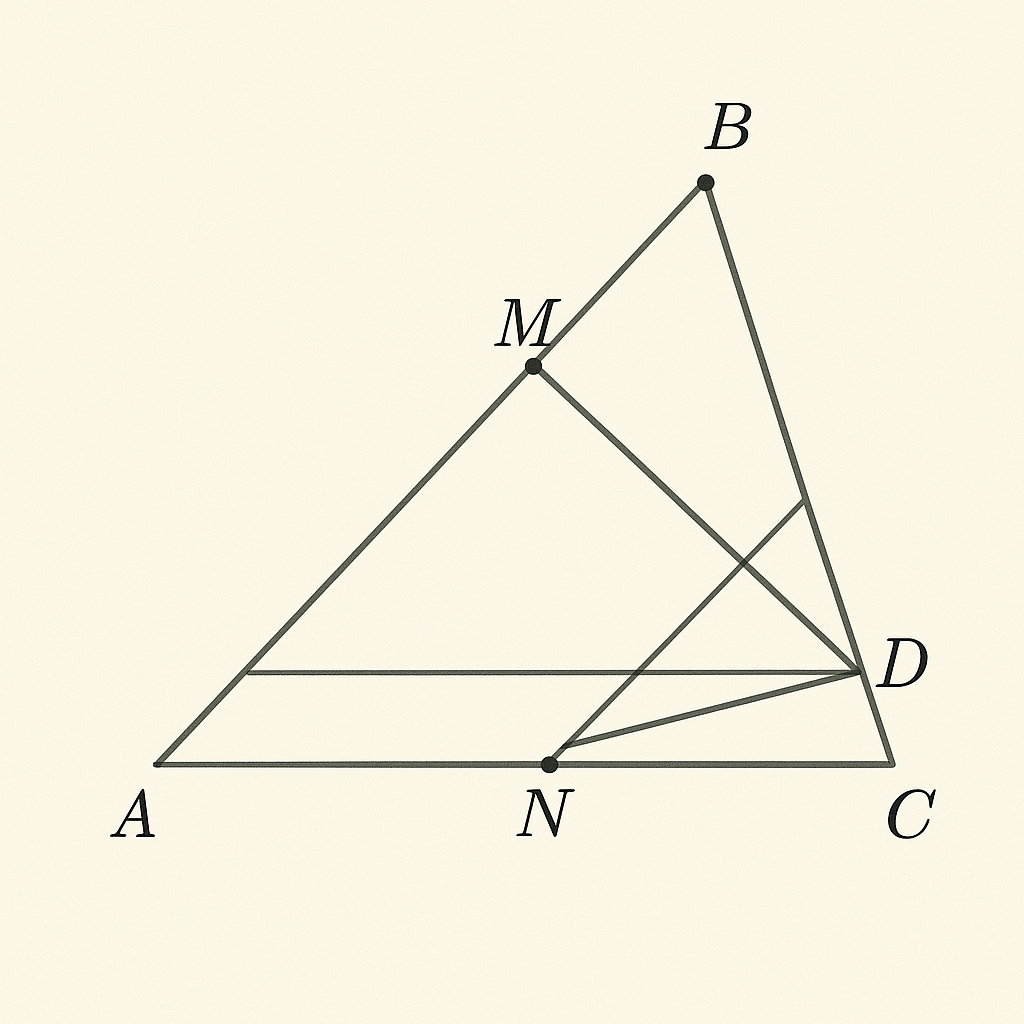
Bài 10
a) Chứng minh tam giác AHBA ∼ tam giác ABC
- Hai tam giác vuông tại A và H
- Có góc chung tại B
=> ΔAHB ∼ ΔABC (g.g)
b) Tính BC và AH
- BC = \( \sqrt{AB^2 + AC^2} = \sqrt{81 + 144} = \sqrt{225} = 15 \) cm
- AH = \( \frac{AB \cdot AC}{BC} = \frac{9 \cdot 12}{15} = \frac{108}{15} = 7,2 \) cm
câu c:
ΔABC vuông tại A ⇒ AH ⊥ BC
=> AH là đường cao từ A
HM = HA, M nằm trên HC ⇒ điểm M là đối xứng của A qua H
=> Vì H là trung điểm của AM
=> Tứ giác AHMC đối xứng trục qua H
MI ⊥ BC, cắt AC tại I
Vì MI ⊥ BC, mà AH cũng ⊥ BC, => MI // AH
. CK ⊥ BC, K nằm trên phân giác ∠IMC
Giao điểm của CK vuông góc với BC và tia phân giác ∠IMC ⇒ điểm K mang tính chất đối xứng, chia đều góc ∠IMC
Mà tam giác IMC có tính chất đối xứng vì:
M đối xứng với A qua H
MI ⊥ BC
CK ⊥ BC
⇒ K nằm đối xứng với I qua H ⇒ K, I, H thẳng hàng
=> H, I, K thẳng hàng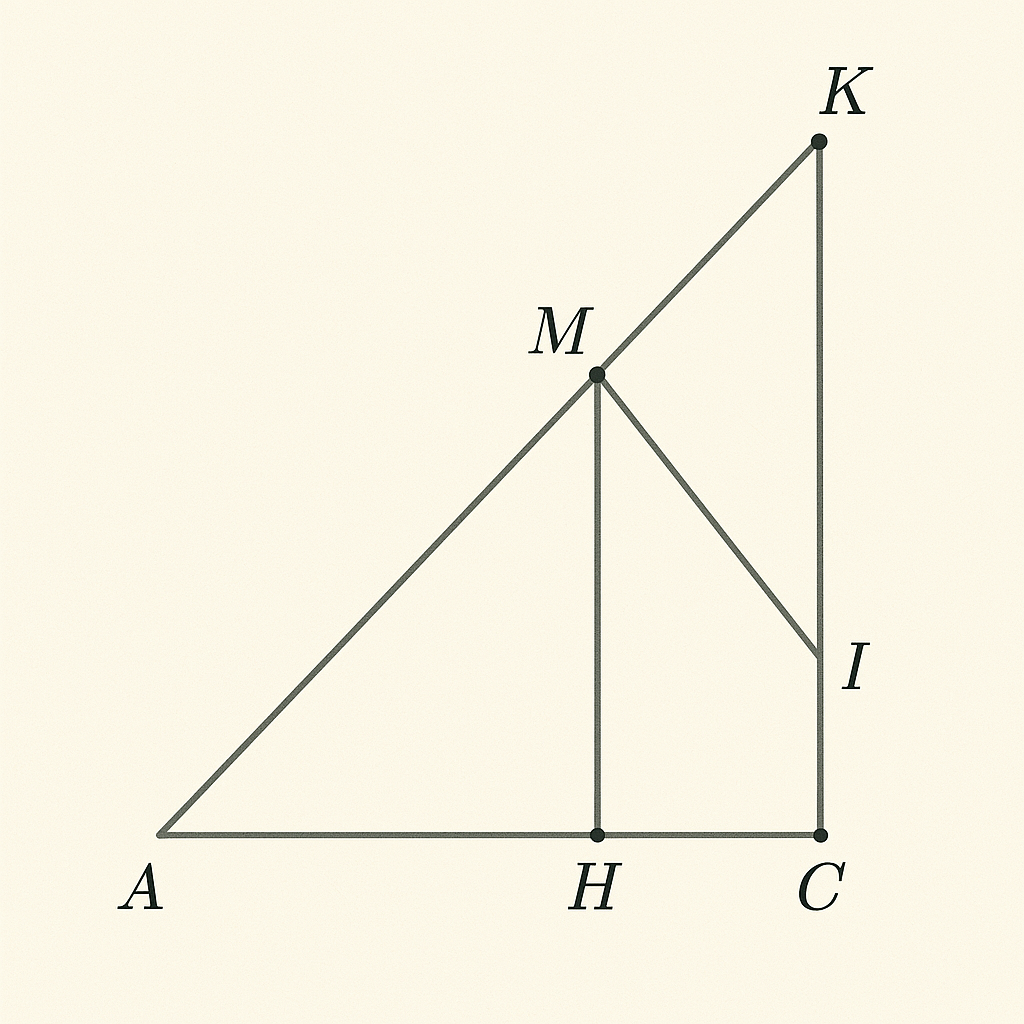
Bài 7
BD là đường trung tuyến đi từ B đến D (trung điểm của AM)
Khi BD cắt AC tại E → điểm E chia AC theo tỉ lệ 2:1
(Tính chất: đường trung tuyến chia đường đối diện theo tỉ lệ 2:1 từ phía đỉnh, dựa vào tính chất trọng tâm tam giác và các đoạn trung tuyến cắt nhau)
Vì AC = 9 cm, nên:
\[
AE = \frac{2}{3} \cdot AC = \frac{2}{3} \cdot 9 = 6 \text{ cm}
\]
Đáp án: AE = 6 cm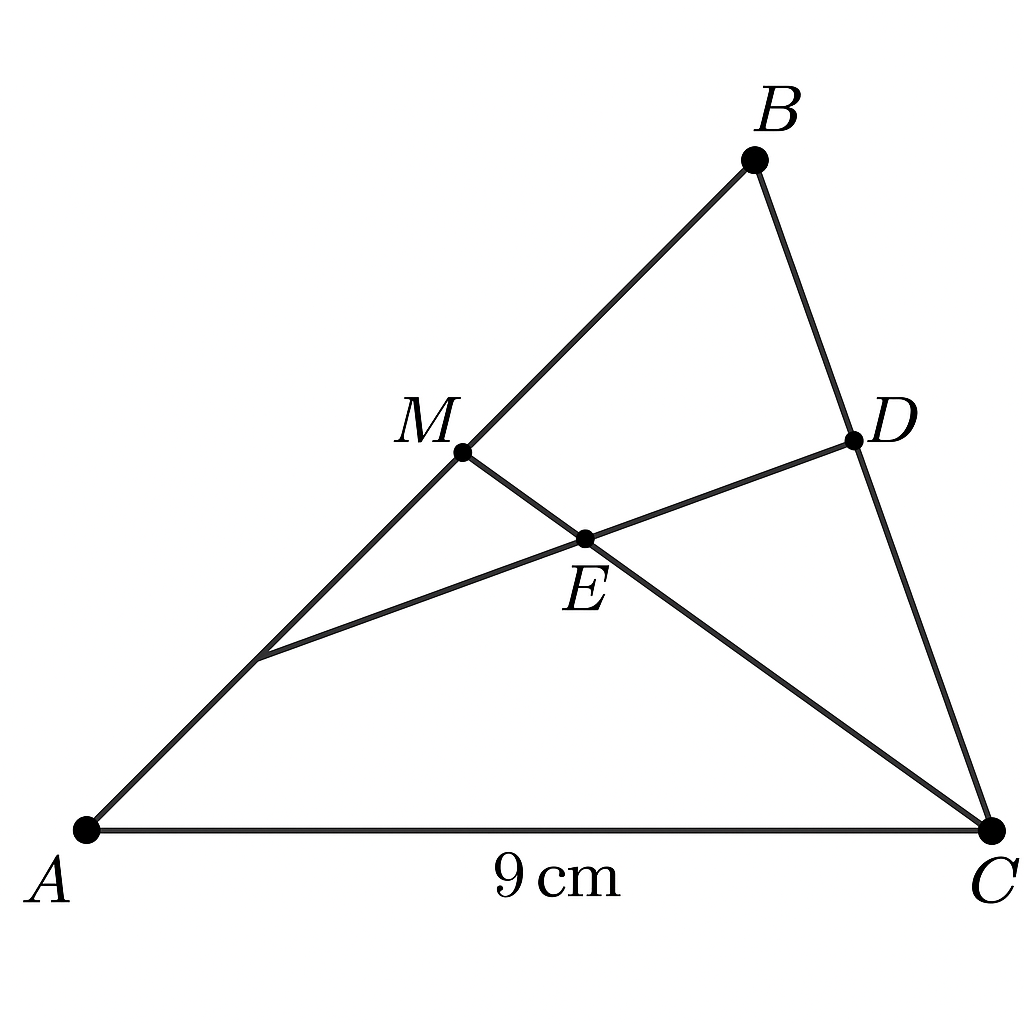
bài 7.
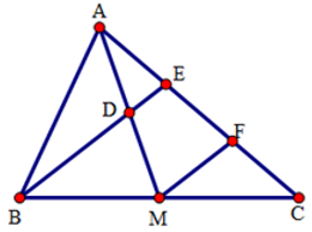
Xét tam giác, AMF có AD = CM, DE // MF
Do đó AE = EF = FC nên AE = AC = .9 = 3 cm
bài 9.
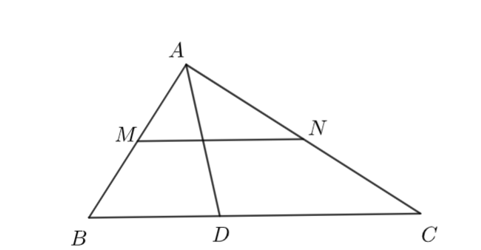
a) Có AD là phân giác của góc BAC nên BD/DC=AB/AC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
BD/DC=AB/AC
=> BD/DC+BD=AB/AC+AB
=> BD/10=6/14
Do đó, BD=10.6/14=30/7cm.
b) Có AD là phân giác của góc BAC nên BD/DC=AB/AC.
Lại có MN ∥ BC
=> AM/AB=AN/AC hay AM/AN=AB/AC
Từ đó => AM/AN=DB/DC hay BD.AN=AM.DC (đpcm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6301
Đã trả lời bởi chuyên gia
6301 -
 Đã trả lời bởi chuyên gia
4621
Đã trả lời bởi chuyên gia
4621 -
 Đã trả lời bởi chuyên gia
4112
Đã trả lời bởi chuyên gia
4112 -
 Đã trả lời bởi chuyên gia
4063
Đã trả lời bởi chuyên gia
4063


