Ta có:
- \( SA \perp (ABC) \Rightarrow SA \perp AB, SA \perp AC \)
- Dựng hệ trục tọa độ để tính góc giữa \( SA \) và mặt phẳng (AMN)

- Gốc tọa độ O trùng điểm A → \( A(0, 0, 0) \)
- \( AB = 1 \), đặt \( B(1, 0, 0) \)
- \( AC = 2 \), \( \angle BAC = 120^\circ \)

Dùng công thức lượng giác để tìm tọa độ C:

- Gọi \( C(x, y, 0) \), ta biết:
\[
AB \cdot AC \cdot \cos\angle BAC = AB \cdot AC \cdot \cos(120^\circ) = 1 \cdot 2 \cdot (-\frac{1}{2}) = -1
\]

Dùng tích vô hướng \( \vec{AB} \cdot \vec{AC} = -1 \)

\[
\vec{AB} = (1, 0), \quad \vec{AC} = (x, y) \Rightarrow 1 \cdot x + 0 \cdot y = x = -1 \Rightarrow x = -1
\]

Lại có: \( AC = 2 \Rightarrow \sqrt{x^2 + y^2} = 2 \)

\[
x = -1 \Rightarrow x^2 = 1 \Rightarrow y^2 = 4 - 1 = 3 \Rightarrow y = \sqrt{3}
\]

⇒ \( C(-1, \sqrt{3}, 0) \)

\( SA = \sqrt{7} \), vuông góc với mặt phẳng đáy ⇒ điểm \( S(0, 0, \sqrt{7}) \)

Xác định vector \( \vec{SA} = (0, 0, -\sqrt{7}) \)

- Tính tọa độ điểm M là hình chiếu của A lên SB:
+ A: (0, 0, 0), S: (0, 0, √7), B: (1, 0, 0)
+ Vector \( \vec{SB} = (1, 0, -\sqrt{7}) \)
+ Gọi M là hình chiếu của A lên SB ⇒ \( \vec{AM} \) vuông góc với \( \vec{SB} \)

Dùng công thức chiếu điểm A lên đường thẳng SB:

\[
\text{Gọi } \vec{u} = \vec{SB} = (1, 0, -\sqrt{7})
\]
\[
\vec{SA} = (0, 0, -\sqrt{7})
\]

Ta chiếu \( \vec{SA} \) lên \( \vec{u} \):

\[
\cos \theta = \frac{|\vec{SA} \cdot \vec{u}|}{|\vec{SA}| \cdot |\vec{u}|}
\]

- \( \vec{SA} \cdot \vec{u} = 0 \cdot 1 + 0 \cdot 0 + (-\sqrt{7}) \cdot (-\sqrt{7}) = 7 \)
- \( |\vec{SA}| = \sqrt{7} \)
- \( |\vec{u}| = \sqrt{1^2 + 0 + 7} = \sqrt{8} \)

\[
\cos \theta = \frac{7}{\sqrt{7} \cdot \sqrt{8}} = \frac{7}{\sqrt{56}} = \frac{7}{\sqrt{56}} \approx \frac{7}{7.4833} \approx 0.9356
\]

Giá trị cosin của góc giữa đường thẳng SA và mặt phẳng (AMN) xấp xỉ:
\[
\boxed{0,94}
\] (làm tròn đến hàng phần trăm)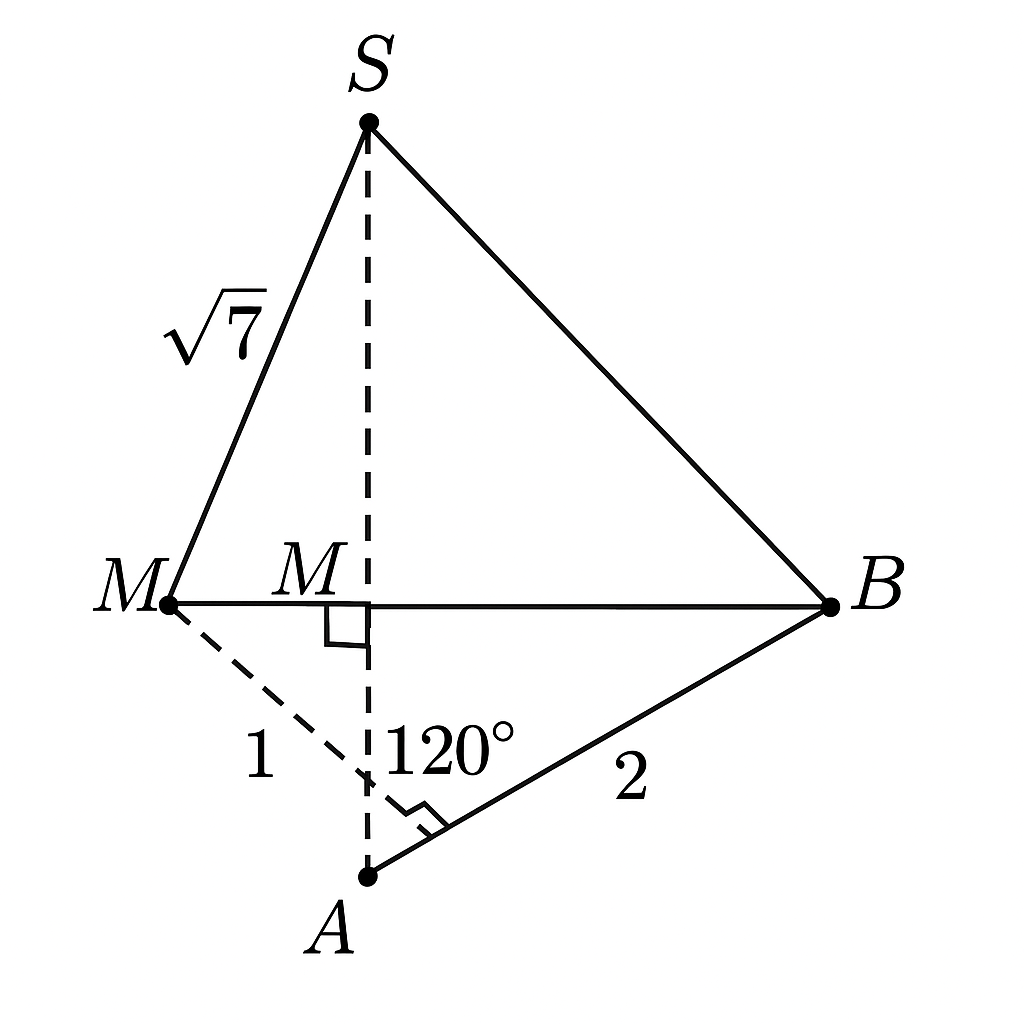 

Xác định các yếu tố cơ bản: