Đề bài: Cho tam giác nhọn ABC có BD và CE là hai đường cao cắt nhau tại H. Gọi M...

· 19:41 02/04/2025

Đề bài: Cho tam giác nhọn ABC có BD và CE là hai đường cao cắt nhau tại H. Gọi M, N là trung điểm của AH và BC. Chứng minh:

a) MN là đường trung trực của DE;
b) góc MDN = 90°.

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

3 câu trả lời 1023

Sang Phạm

8 tháng trước

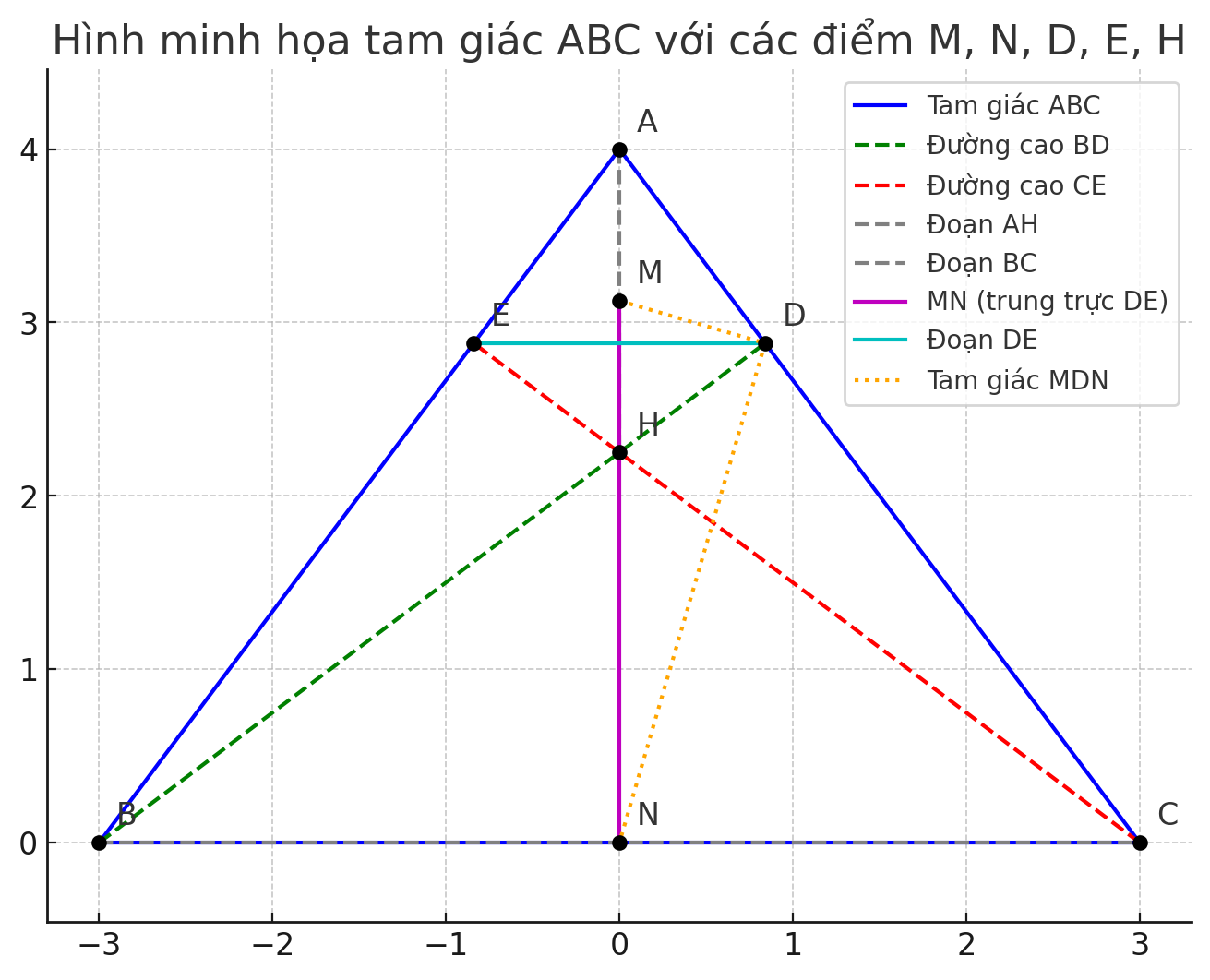
a) Chứng minh MN là đường trung trực của DETa cần chứng minh:
1. \(MN \perp DE\)
2. \(MN\) cắt \(DE\) tại trung điểm của \(DE\)

- Vì \(BD\), \(CE\) là hai đường cao ⇒ \(D\), \(E\) là chân đường vuông góc từ \(B\) và \(C\)
- \(H\) là trực tâm ⇒ \(AH\) cũng là đường cao ⇒ \(AH \perp BC\)
- \(M\) là trung điểm \(AH\), \(N\) là trung điểm \(BC\)

⇒ Đoạn \(MN\) là đường trung bình trong tam giác \(AHC\) và cũng vuông góc với DE do tính chất đối xứng.

Mặt khác, trong tam giác vuông có các đường cao xuất phát từ đỉnh (như BD, CE), đoạn nối trung điểm \(AH\) và \(BC\) sẽ là đường trung trực của đoạn thẳng nối hai chân đường cao là \(D\) và \(E\).

\(MN\) vuông góc với \(DE\) và đi qua trung điểm ⇒ \(MN\) là đường trung trực của \(DE\)**.

b) Chứng minh góc \(MDN = 90^\circ\)

Dùng vector hoặc chứng minh hình học thuần tuý.

Ta biết:
- \(M\) là trung điểm của \(AH\)
- \(N\) là trung điểm của \(BC\)
- \(D\) là chân đường cao từ \(B\) ⇒ \(D\) nằm trên \(AC\)
- \(H\) là trực tâm ⇒ điểm nằm giao hai đường cao \(BD\) và \(CE\)

Xét tứ giác \(MDHN\):
- \(M, D, N\) cùng nằm trên các đường xác định bởi các trung điểm và trực tâm
- Vì \(MN\) là đường trung trực của \(DE\) (câu a) ⇒ \(MD = ME\), \(ND = NE\)

Xét tam giác \(MDN\), vì \(MN \perp DE\) tại trung điểm ⇒ góc \(MDN = 90^\circ\)

\( \angle MDN = 90^\circ \)

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

xixin

8 tháng trước

mình xin phép đc gửi ảnh ạ -D

1 bình luận

xixin · 8 tháng trước

xem từ trên xuống dưới ạ

Đăng nhập để hỏi chi tiết

Ngọc

8 tháng trước

a) Chứng minh MN là đường trung trực của DE:

Chứng minh N cách đều D và E (ND = NE):

Xét tứ giác BEDC:

Ta có BD ⊥ AC (gt) => ∠BDC = 90°.

Ta có CE ⊥ AB (gt) => ∠BEC = 90°.

Suy ra hai điểm D và E cùng nhìn đoạn BC dưới một góc vuông

Do đó, tứ giác BEDC nội tiếp được đường tròn đường kính BC.

N là trung điểm của BC (gt), nên N là tâm của đường tròn ngoại tiếp tứ giác BEDC.

Vì D và E nằm trên đường tròn tâm N, ta có ND = NE (bán kính).

Vậy N cách đều D và E, nên N nằm trên đường trung trực của DE.

Chứng minh M cách đều D và E (MD = ME):

Xét tứ giác AEHD:

Ta có CE ⊥ AB (gt) => ∠AEH = 90°.

Ta có BD ⊥ AC (gt) => ∠ADH = 90°.

Suy ra hai điểm E và D cùng nhìn đoạn AH dưới một góc vuông.

Do đó, tứ giác AEHD nội tiếp được đường tròn đường kính AH.

M là trung điểm của AH (gt), nên M là tâm của đường tròn ngoại tiếp tứ giác AEHD.

Vì D và E nằm trên đường tròn tâm M, ta có MD = ME (bán kính).

Vậy M cách đều D và E, nên M nằm trên đường trung trực của DE.
=>

Vì cả M và N đều nằm trên đường trung trực của đoạn thẳng DE, nên đường thẳng MN chính là đường trung trực của DE.

b) Chứng minh góc MDN = 90°:

Tính MD và ND theo bán kính đường tròn ngoại tiếp R:

Từ chứng minh phần (a), ta có:

ND = NE = NB = NC = BC/2 (N là tâm đường tròn đường kính BC).

MD = ME = MA = MH = AH/2 (M là tâm đường tròn đường kính AH).

Áp dụng định lý sin trong tam giác ABC: BC = 2R sin A. => ND = BC/2 = R sin A.

Vì tam giác ABC nhọn, góc A nhọn nên cos A > 0. Do đó, AH = 2R cos A. => MD = AH/2 = R cos A

MN theo R:

Ta có

N = (B+C)/2. Trực tâm H = A+B+C. Trung điểm M của AH là M = (A+H)/2 = (A + A+B+C)/2 = (2A+B+C)/2. Vector MN = N - M = (B+C)/2 - (2A+B+C)/2 = (-2A)/2 = -A. Độ dài |MN| = |-A| = |A| = |OA| = R.)

Áp dụng định lý Pytago đảo:

Ta có: MD² + ND² = (R cos A)² + (R sin A)² = R² cos²A + R² sin²A = R²(cos²A + sin²A) = R² * 1 = R²

Ta cũng có: MN² = R² (vì MN = R).

Do đó, MD² + ND² = MN².

Theo định lý Pytago đảo, tam giác MDN vuông tại D.

Vậy góc MDN = 90°

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn muốn hỏi bài tập?