Cho tam giác MNP vuông tại M có góc P=30độ.Đường trung trực của NP cắt MP tại Q. Chứng minh rằng NQ là phân giác của MNP.
giúp
Quảng cáo
3 câu trả lời 604
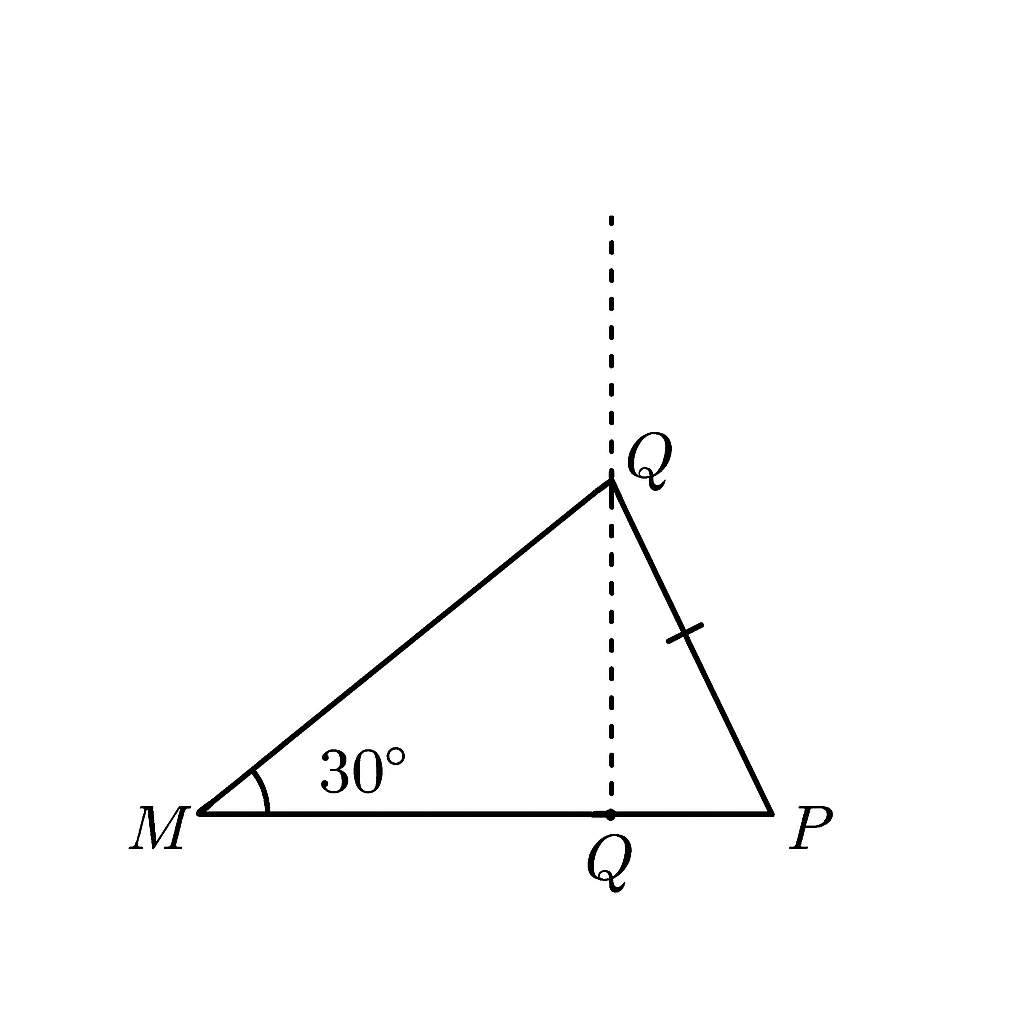
Tam giác vuông tại M → \( \angle M = 90^\circ \)
\( \angle P = 30^\circ \) ⇒ \( \angle N = 60^\circ \) (vì tổng góc tam giác là 180°)
- Vì O là trung điểm và Q nằm trên trung trực của NP ⇒ \( QN = QP \)
(Định nghĩa trung trực: gồm các điểm cách đều hai đầu đoạn thẳng)
- \( QN = QP \) ⇒ tam giác \( QNP \) cân tại Q
⇒ \( \angle NQP = \angle PQN \)
- \( Q \) nằm trên đoạn \( MP \), nên \( \angle NQM \) và \( \angle MQP \) là các góc kề nhau tạo thành góc \( \angle NQP \)
- Ta chứng minh \( \angle MQN = \angle PQN \)
⇒ \( NQ \) chia \( \angle MNP \) thành 2 phần bằng nhau
Vì \( QN = QP \), nên \( \triangle QNP \) cân tại Q
⇒ \( NQ \) là phân giác của góc \( \angle MNP \)
Vậy NQ là phân giác của \( \angle MNP \)
Xét tam giác MNP vuông tại M có:
=> Góc N = 90 độ - 30 độ = 60 độ
Q thuộc đường trung trực của NP nên QN = QP
=> tam giác NQP cân tại Q
=> Góc QNP = góc QPN = 30 độ
Góc MNQ = góc MNP - góc QNP = 60 độ - 30 độ = 30 độ
=> Góc MNQ = góc QNP = 30 độ
=> NQ là phân giác của góc MNP
Tính góc MNP:
tính chất đường trung trực nên ta có
Xét tam giác NQP:
So sánh các góc và kết luận:
Do đó:
∠MNQ + ∠QNP = ∠MNP ∠MNQ + 30° = 60° ∠MNQ = 60° - 30° = 30°
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


