Cho tam giác ABC có trọng tâm G gọi a'b'c' lần lượt là trung điểm của agbg CG chứng minh tam giác a'b'c' đồng dạng tam giác ABC
Quảng cáo
2 câu trả lời 129
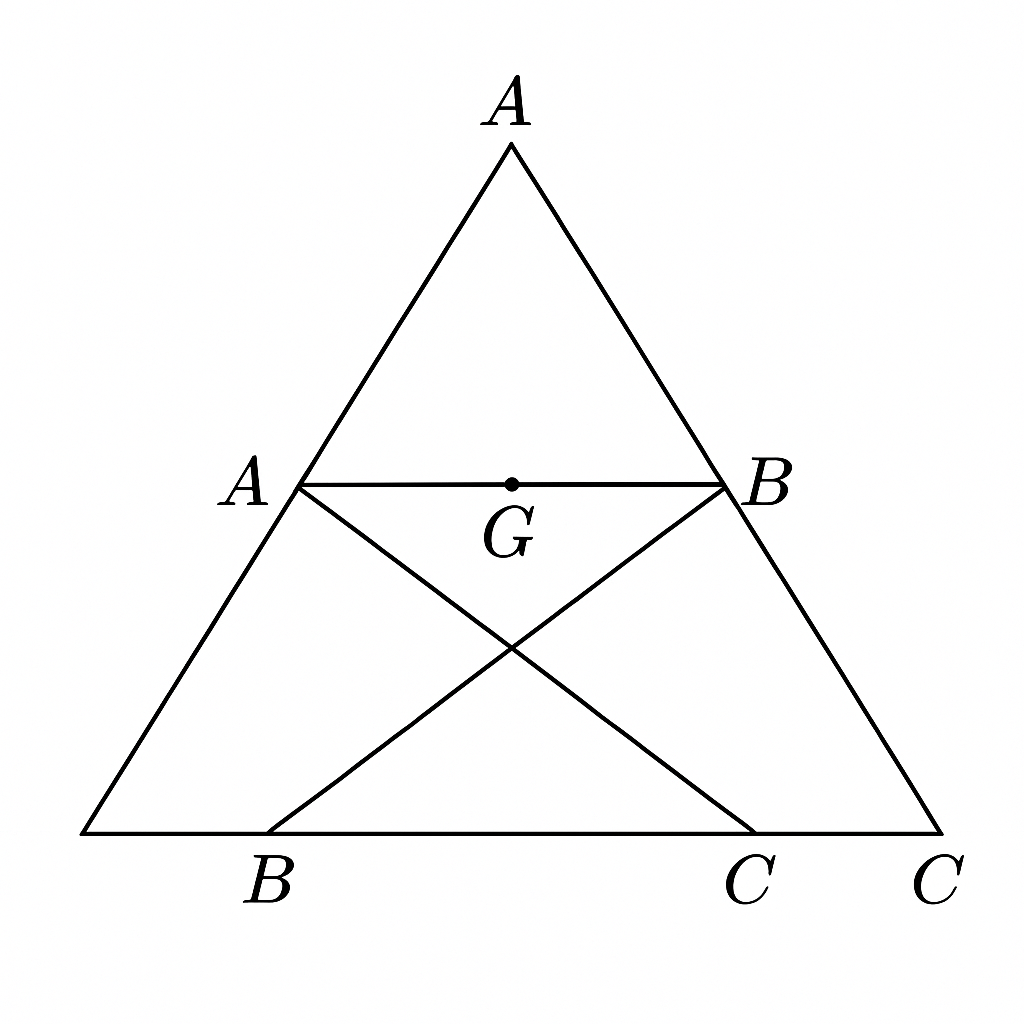
Ta biết:
- \( G \) là trọng tâm tam giác \( ABC \) ⇒ \( G \) chia mỗi trung tuyến theo tỉ lệ \( AG : GM = 2 : 1 \)
- \( A' \) là trung điểm của \( AG \) ⇒ \( \vec{AA'} = \frac{1}{2} \vec{AG} = \frac{1}{3} \vec{AM} \), do \( AG = \frac{2}{3} AM \)
Tương tự:
- \( A' = \text{trung điểm}(AG) \Rightarrow \vec{GA'} = \frac{1}{2} \vec{GA} \)
- \( B' = \text{trung điểm}(BG) \Rightarrow \vec{GB'} = \frac{1}{2} \vec{GB} \)
- \( C' = \text{trung điểm}(CG) \Rightarrow \vec{GC'} = \frac{1}{2} \vec{GC} \)
Xét vector \( \vec{A'B'} \):
\[
\vec{A'B'} = \vec{A'G} + \vec{GB'} = -\frac{1}{2}\vec{GA} + \frac{1}{2} \vec{GB} = \frac{1}{2}(\vec{GB} - \vec{GA}) = \frac{1}{2} \vec{AB}
\]
Tương tự:
- \( \vec{B'C'} = \frac{1}{2} \vec{BC} \)
- \( \vec{C'A'} = \frac{1}{2} \vec{CA} \)
- Tam giác \( A'B'C' \) có các cạnh tỉ lệ với tam giác \( ABC \): tỉ lệ \( \frac{1}{2} \)
- Các cặp cạnh tương ứng song song và cùng hướng
→ Tam giác \( A'B'C' \) đồng dạng với tam giác \( ABC \) (tỉ lệ \( \dfrac{1}{2} \))
Q.E.D – Điều phải chứng minh.
Xét tam giác ABG:
Xét tam giác BCG:
Xét tam giác ACG:
Tương tự, theo định lý đường trung bình trong tam giác ACG, ta có:
A'B' / AB = B'C' / BC = A'C' / AC = 1/2
Tam giác A'B'C' đồng dạng với tam giác ABC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


