cho hình chữ nhật ABCD (AB<AD). Lấy điểm M thuộc cạnh AB (AM>BM); M không trùng B). tia DM cắt tia CB tại N a) chứng minh tam giác MBN đồng dạng với tam giác MAD b) chứng minh tam giác ADM đồng dạng với tam giác CND từ đó chứng minh BC.CD=AM.NC c) qua M kẻ đường thẳng vuông góc với DN, đường thẳng này cắt tia NC tại E. chứng minh góc NMC = góc NED
Quảng cáo
2 câu trả lời 92
a) Chứng minh tam giác MBN ∽ tam giác MAD
Xét tam giác MBN và tam giác MAD:
- ∠MBN và ∠MAD là đối đỉnh ⇒ bằng nhau
- ∠BMN và ∠ADM là góc chung
⇒ ΔMBN ∽ ΔMAD (g.g)
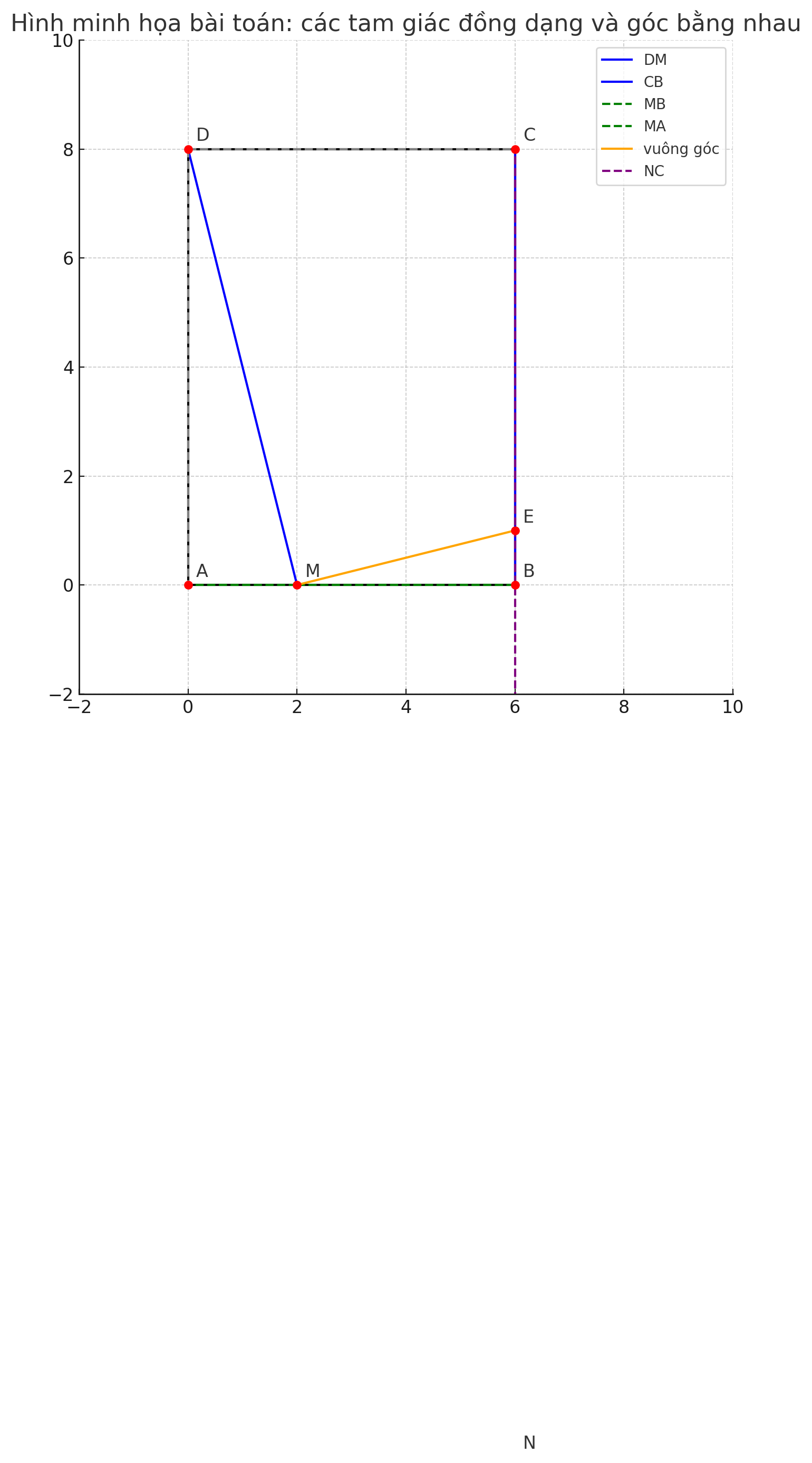
b) Chứng minh ΔADM ∽ ΔCND ⇒ suy ra BC.CD = AM.NC
Xét tam giác ADM và tam giác CND:
- ∠ADM = ∠CND (đối đỉnh)
- ∠MAD = ∠NCD (đồng vị vì AB // DC, cùng cắt bởi tia DN)
⇒ ΔADM ∽ ΔCND (g.g)
Từ đó, ta có tỉ lệ đồng dạng:
AMNC=ADCD⇒AM⋅CD=NC⋅AD
Mà AD = BC (vì ABCD là hình chữ nhật)
⇒ BC · CD = AM · NC
c) Qua M kẻ đường thẳng vuông góc với DN, cắt tia NC tại E. Chứng minh ∠NMC = ∠NED
- Kẻ ME vuông góc với DN ⇒ ∠NME = 90°
- ∠NED = 90° (vì cùng vuông góc với DN)
- Hai góc ∠NMC và ∠NED cùng chắn cung NC (hoặc cùng phụ nhau với góc 90° theo ME)
⇒ ∠NMC = ∠NED (đồng vị hoặc bằng nhau do cùng phụ góc vuông)
Quảng cáo
Câu hỏi hot cùng chủ đề
-
103881
-
Hỏi từ APP VIETJACK60597
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức MH2=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
44040

 đây ạ
đây ạ 


![CEO tập đoàn Lục thị[nk]](/upload/images/user/1757779274-anh-chup-man-hinh-2025-09-09-000613png.png)








