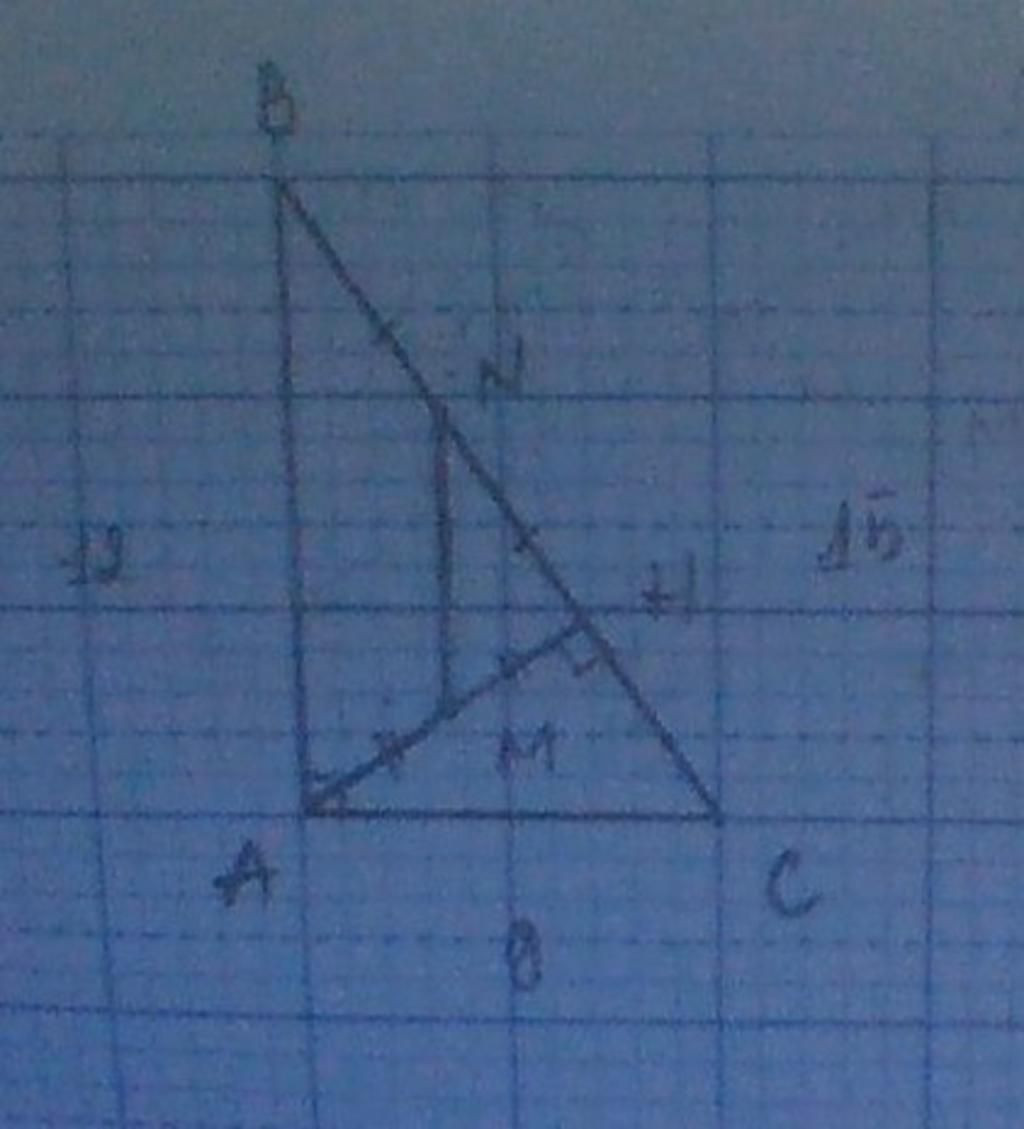
a) CM tam giác ABC vuông tại A
b)CM HNM đồng dạng với tam giác ABC
Quảng cáo
3 câu trả lời 93
a) Chứng minh tam giác ABC vuông tại A:
Tính bình phương các cạnh:
AB² = 12² = 144
AC² = 9² = 81
BC² = 15² = 225
Kiểm tra định lý Pytago đảo:
Ta thấy: AB² + AC² = 144 + 81 = 225
Và BC² = 225
Vậy AB² + AC² = BC²
Kết luận:
Theo định lý Pytago đảo, tam giác ABC vuông tại A.
b) Chứng minh tam giác HNM đồng dạng với tam giác ABC:
Xét tam giác HNM:
M là trung điểm AH, N là trung điểm BH.
Suy ra MN là đường trung bình của tam giác ABH.
Do đó, MN // AB và MN = 1/2 AB.
Góc HNM = góc ABH (hai góc đồng vị).
Xét tam giác ABC:
Góc BAC = 90° (chứng minh ở câu a).
Góc ABH chung.
So sánh hai tam giác:
Xét tam giác HNM và tam giác ABC:Góc HNM = góc ABH (chứng minh trên).
Góc MHN = góc BAC = 90° (AH ⊥ BC).
Vậy tam giác HNM đồng dạng với tam giác ABC (g.g).
Kết luận:
a) Tam giác ABC vuông tại A.
b) Tam giác HNM đồng dạng với tam giác ABC.
## Giải bài toán:
**a) Chứng minh tam giác ABC vuông tại A**
Ta có:
* AC2=92=81
* AB2=122=144
* BC2=152=225
Nhận thấy: AC2+AB2=81+144=225=BC2
Vậy, theo định lý Py-ta-go đảo, tam giác ABC vuông tại A.
**b) Chứng minh tam giác HNM đồng dạng với tam giác ABC**
Xét tam giác AHB vuông tại H, có N là trung điểm của BH:
=> HN = 12 BH (1)
Mà M là trung điểm của AH:
=> HM = 12 AH (2)
Từ (1) và (2) suy ra HNBH=HMAH=12
Xét tam giác HNM và tam giác AHB, có:
* ∠H chung
* HNBH=HMAH (chứng minh trên)
=> Tam giác HNM đồng dạng với tam giác AHB (c.g.c)
=> ∠HNM=∠ABH
Mà ∠ABH+∠ACB=90∘ (do tam giác ABC vuông tại A)
=> ∠HNM+∠ACB=90∘
Lại có: ∠MHN=90∘
=> ∠HNM+∠HMN=90∘
=> ∠HMN=∠ACB
Xét tam giác HNM và tam giác ABC, có:
* ∠MHN=∠BAC=90∘
* ∠HMN=∠ACB (chứng minh trên)
=> Tam giác HNM đồng dạng với tam giác ABC (g.g)
Quảng cáo
Câu hỏi hot cùng chủ đề
-
101465
-
Hỏi từ APP VIETJACK52579
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức
=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
43223