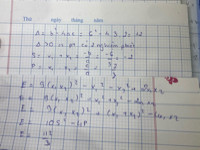a) chứng tỏ ptrinh luôn có 2 nghiệm phân biệt
b) tính giá trị biểu thức E= 9x1^2.x2^2 -x1^2 - x2^2
Quảng cáo
2 câu trả lời 849
Để làm bài này, chúng ta có phương trình bậc hai:
3x2+6x+2=03x^2 + 6x + 2 = 03x2+6x+2=0
a) Chứng tỏ phương trình luôn có 2 nghiệm phân biệt
Để chứng tỏ rằng phương trình bậc hai ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0 luôn có hai nghiệm phân biệt, chúng ta sử dụng điều kiện của delta (D).
Công thức tính delta:
D=b2−4acD = b^2 - 4acD=b2−4ac
Áp dụng vào phương trình:
a=3a = 3a=3
b=6b = 6b=6
c=2c = 2c=2
Tính delta:
D=62−4⋅3⋅2=36−24=12D = 6^2 - 4 \cdot 3 \cdot 2 = 36 - 24 = 12D=62−4⋅3⋅2=36−24=12
Vì D>0D > 0D>0, điều này chứng tỏ rằng phương trình bậc hai này có hai nghiệm phân biệt.
b) Tính giá trị biểu thức E=9x12x22−x12−x22E= 9x_1^2 x_2^2 - x_1^2 - x_2^2E=9x12x22−x12−x22
Để tính giá trị biểu thức EEE, chúng ta có thể sử dụng định lý Viète:
Theo định lý Viète, đối với phương trình bậc hai ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0, ta có:Tổng hai nghiệm x1+x2=−ba=−63=−2x_1 + x_2 = -\frac{b}{a} = -\frac{6}{3} = -2x1+x2=−ab=−36=−2
Tích hai nghiệm x1x2=ca=23x_1 x_2 = \frac{c}{a} = \frac{2}{3}x1x2=ac=32
Chúng ta có thể tính x12+x22x_1^2 + x_2^2x12+x22 bằng cách sử dụng công thức:
x12+x22=(x1+x2)2−2x1x2x_1^2 + x_2^2 = (x_1 + x_2)^2 - 2x_1 x_2x12+x22=(x1+x2)2−2x1x2
x12+x22=(−2)2−2⋅23=4−43=123−43=83x_1^2 + x_2^2 = (-2)^2 - 2 \cdot \frac{2}{3} = 4 - \frac{4}{3} = \frac{12}{3} - \frac{4}{3} = \frac{8}{3}x12+x22=(−2)2−2⋅32=4−34=312−34=38
Bây giờ, ta cần tính x12x22x_1^2 x_2^2x12x22:
x12x22=(x1x2)2=(23)2=49x_1^2 x_2^2 = (x_1 x_2)^2 = \left( \frac{2}{3} \right)^2 = \frac{4}{9}x12x22=(x1x2)2=(32)2=94
Đưa tất cả vào biểu thức EEE:
E=9x12x22−x12−x22E = 9x_1^2 x_2^2 - x_1^2 - x_2^2E=9x12x22−x12−x22
E=9⋅49−83E = 9 \cdot \frac{4}{9} - \frac{8}{3}E=9⋅94−38
E=4−83E = 4 - \frac{8}{3}E=4−38
Để thực hiện phép trừ, quy đồng mẫu số:
E=123−83=43E = \frac{12}{3} - \frac{8}{3} = \frac{4}{3}E=312−38=34
Kết quả
a) Phương trình luôn có 2 nghiệm phân biệt.
b) Giá trị của biểu thức EEE là 43\frac{4}{3}34.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274