Quảng cáo
2 câu trả lời 1206
a) Tứ giác AICK là hình gì? Vì sao?
Trong tam giác ABCABC, ta có:
MM là trung điểm của AB,
NN là trung điểm của AC,
Tia phân giác của góc A cắt BC tại I,
NN là trung điểm của đoạn IK.
Ta cần chứng minh tứ giác AICK là hình gì.
Chứng minh:
Vì N là trung điểm của AC, và N là trung điểm của IK, ta có:
$\overrightarrow{IN}$ = $\overrightarrow{NK}$.
Do M là trung điểm của AB, ta có:
$\overrightarrow{AM}$ = $\overrightarrow{MB}$.
Ta sẽ dùng các tính chất về trung điểm và phân giác. Trong tam giác, nếu một điểm thuộc tia phân giác của một góc, thì tỷ lệ giữa các đoạn mà tia phân giác chia đoạn đối diện bằng tỷ lệ các cạnh kề của tam giác. Cụ thể, ta có:
$\frac{BI}{IC}$ = $\frac{AB}{AC}$.
Ta có thể thấy rằng, với các điều kiện đã cho, AICK là một hình thang (hình thang vuông nếu A, C, K cùng một đường thẳng).
b) Chứng minh IB $\cdot$ NC = IC $\cdot$ MB
Chứng minh này áp dụng định lý phân giác trong tam giác và tính chất các đoạn thẳng.
Chứng minh:
Tia phân giác của góc A chia cạnh BC tại điểm I, do đó theo định lý phân giác, ta có:
$\frac{BI}{IC}$ = $\frac{AB}{AC}$.
Ta có M là trung điểm của AB, nên MB = $\frac{AB}{2}$.
Ta có N là trung điểm của AC, nên NC = $\frac{AC}{2}$.
Áp dụng định lý phân giác với các đoạn thẳng đã biết:
$\frac{BI}{IC}$ = $\frac{AB}{AC}$ = $\frac{2MB}{2NC}$ = $\frac{MB}{NC}$.
Từ đó, ta suy ra:
IB $\cdot$ NC = IC $\cdot$ MB.
Vậy ta đã chứng minh được điều cần chứng minh.
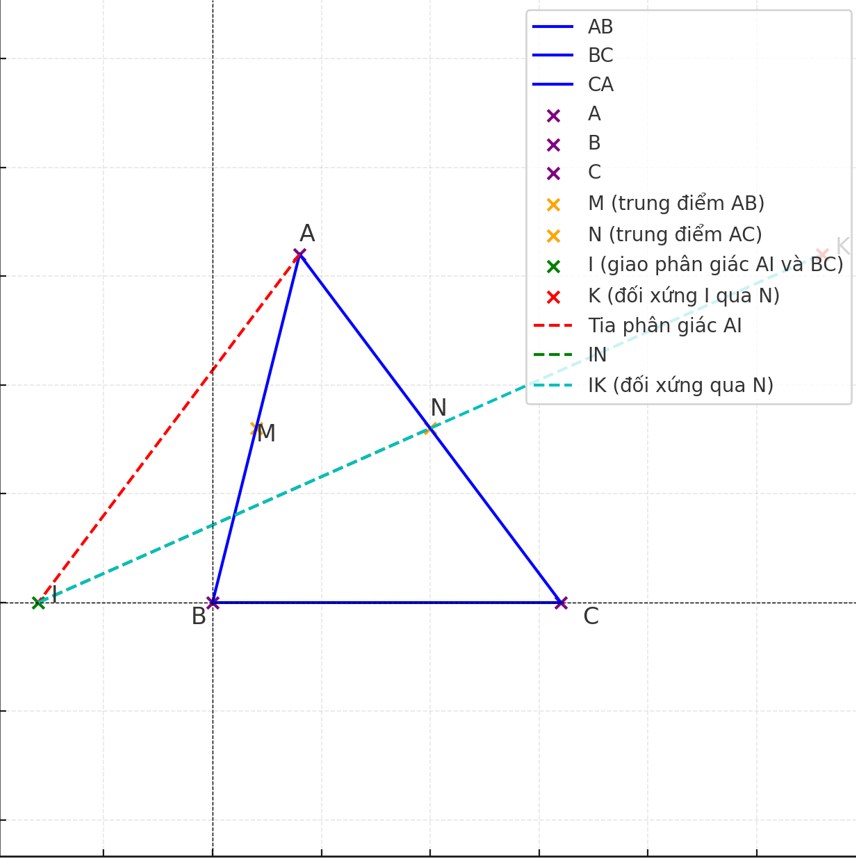
a) Tứ giác AICK là hình bình hành.
N là trung điểm của AC và IK (theo giả thiết)
Do đó, tứ giác AICK có hai đường chéo AC và IK cắt nhau tại trung điểm N của mỗi đường
Theo tính chất tứ giác, tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành
=>tứ giác AICK là hình bình hành.
b) Chứng minh IB.NC = IC.MB
Xét tam giác ABC:
M là trung điểm của AB (giả thiết)
N là trung điểm của AC (giả thiết)
Theo tính chất đường trung bình của tam giác, MN là đường trung bình của tam giác ABC.
MN là đường trung bình => MN // BC.
Xét tam giác AMN và tam giác ABC:
Góc A chung
Góc AMN = Góc ABC (hai góc đồng vị do MN // BC)
Góc ANM = Góc ACB (hai góc đồng vị do MN // BC)
=> Tam giác AMN đồng dạng với tam giác ABC (g.g.g)
Tam giác AMN đồng dạng với tam giác ABC => AM/AB = AN/AC = MN/BC.
Mà AM = 1/2 AB (M là trung điểm AB)
Và AN = 1/2 AC (N là trung điểm AC)
=> MN/BC = 1/2 => MN = 1/2 BC.
AI là tia phân giác của góc A (giả thiết) => Theo tính chất đường phân giác trong tam giác:
IB/IC = AB/AC
M là trung điểm AB => MB = 1/2 AB => AB = 2MB.
N là trung điểm AC => NC = 1/2 AC => AC = 2NC.
Thay AB = 2MB và AC = 2NC vào IB/IC = AB/AC:
IB/IC = 2MB/2NC
IB/IC = MB/NC
Nhân chéo:
IB.NC = IC.MB (đpcm)
Kết luận: IB.NC = IC.MB
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107742
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68485
Đã trả lời bởi chuyên gia
68485 -
 Đã trả lời bởi chuyên gia
52942
Đã trả lời bởi chuyên gia
52942 -
 Đã trả lời bởi chuyên gia
47433
Đã trả lời bởi chuyên gia
47433 -
 Đã trả lời bởi chuyên gia
45529
Đã trả lời bởi chuyên gia
45529 -
 Đã trả lời bởi chuyên gia
45189
Đã trả lời bởi chuyên gia
45189 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38558
Đã trả lời bởi chuyên gia
38558 -
 Đã trả lời bởi chuyên gia
38279
Đã trả lời bởi chuyên gia
38279


