Cho tam giác ABC cân tại A đường cao AH. Gọi M là trung điểm của AB và E là điểm đối xứng với H qua M
Cho tam giác ABC cân tại A đường cao AH. Gọi M là trung điểm của AB và E là điểm đối xứng với H qua M .
a) Chứng minh AHBE là hình chữ nhật
b) Chứng minh ACHE là hình bình hành
c)trên tia AH lấy điểm F sao cho HA=HF.KH vuông góc với FB tại K,gọi I là trung điểm của HK.kẻ IJ//BC(J thuộc BF).chứng minh rằng CK vuông góc với FI
Quảng cáo
2 câu trả lời 448
Chúng ta sẽ giải lần lượt từng phần của bài toán này.
### a) Chứng minh AHBE là hình chữ nhật
1. **Gọi các điểm và trung điểm:**
- \( M \) là trung điểm của \( AB \).
- \( E \) là điểm đối xứng với \( H \) qua \( M \).
2. **Tính chất đối xứng:**
- \( M \) là trung điểm của \( AB \) nên \( AM = MB \).
- Vì \( E \) là điểm đối xứng với \( H \) qua \( M \), nên \( MH = ME \) và \( M, H, E \) thẳng hàng.
3. **Chứng minh các cạnh song song và bằng nhau:**
- Tam giác \( ABC \) cân tại \( A \) nên \( AH \) là đường cao và cũng là đường trung tuyến, do đó \( AH \perp BC \).
- \( AM = MB \) và \( ME = MH \), do đó \( AE = BH \).
- Tứ giác \( AHBE \) có:
- \( AH \perp BE \)
- \( AE \perp BH \)
- \( AH = BE \)
- \( AE = BH \)
=> Vậy \( AHBE \) là hình chữ nhật vì có hai cặp cạnh đối song song và bằng nhau, và các góc vuông.
### b) Chứng minh ACHE là hình bình hành
1. **Tính chất đối xứng và trung điểm:**
- \( C \) là điểm trên cạnh \( BC \), đường cao \( AH \) cắt \( BC \) tại \( H \), do đó \( AH \perp BC \).
2. **Chứng minh các cạnh song song và bằng nhau:**
- \( AE \parallel HC \) vì \( E \) là điểm đối xứng với \( H \) qua \( M \) nên \( AE \parallel HC \) và \( AE = HC \).
- \( AH = EC \) vì \( H \) và \( E \) đối xứng qua \( M \).
=> Tứ giác \( ACHE \) có các cạnh đối song song và bằng nhau, do đó là hình bình hành.
### c) Chứng minh CK vuông góc với FI
1. **Xác định điểm \( F \) và \( K \):**
- Trên tia \( AH \) lấy điểm \( F \) sao cho \( HA = HF \).
- \( KH \perp FB \) tại \( K \).
2. **Điểm \( I \) là trung điểm của \( HK \), và kẻ \( IJ \parallel BC \) với \( J \) thuộc \( BF \):**
- Vì \( I \) là trung điểm của \( HK \), ta có \( HI = IK \).
- \( IJ \parallel BC \).
3. **Chứng minh \( CK \) vuông góc với \( FI \):**
- Do \( F \) là điểm đối xứng với \( A \) qua \( H \), nên \( H \) là trung điểm của \( AF \).
- \( K \) là giao điểm của \( AF \) và \( KH \perp FB \).
- \( I \) là trung điểm của \( HK \), do đó, \( HI = IK \).
- Vì \( IJ \parallel BC \), \( J \) thuộc \( BF \), chúng ta có \( I \) và \( J \) đối xứng nhau qua \( H \).
Do đó, \( CK \) vuông góc với \( FI \) vì \( FI \parallel BC \) và \( BC \perp CK \).
Hy vọng điều này giúp ích cho bạn! Nếu bạn có thêm câu hỏi hoặc cần giải thích thêm chi tiết nào khác, hãy cho mình biết nhé! 😊📚✨
Bạn có cần thêm sự trợ giúp nào khác không?
a) Chứng minh AHBE là hình chữ nhật:
Xác định tứ giác AHBE là hình bình hành:
M là trung điểm của AB (gt)
E là điểm đối xứng với H qua M => M là trung điểm của HE.
Tứ giác AHBE có hai đường chéo AB và HE cắt nhau tại trung điểm M của mỗi đường.
Kết luận: AHBE là hình bình hành (dấu hiệu nhận biết hình bình hành).
Chứng minh AHBE có một góc vuông:
ΔABC cân tại A, AH là đường cao => AH ⊥ BC tại H.
=> Góc AHB = 90 độ.
Kết luận AHBE là hình chữ nhật:
AHBE là hình bình hành (chứng minh trên)
Góc AHB = 90 độ (chứng minh trên)
Kết luận: AHBE là hình chữ nhật (hình bình hành có một góc vuông là hình chữ nhật).
b) Chứng minh ACHE là hình bình hành:
Sử dụng tính chất hình chữ nhật AHBE:
AHBE là hình chữ nhật (chứng minh trên) => AE // BH và AE = BH.
Sử dụng tính chất tam giác cân ABC:
ΔABC cân tại A, AH là đường cao => AH cũng là đường trung tuyến => H là trung điểm của BC => BH = HC.
Kết hợp các điều kiện:
AE // BH (cmt) và BH // HC (cùng thuộc BC) => AE // HC.
AE = BH (cmt) và BH = HC (cmt) => AE = HC.
Kết luận ACHE là hình bình hành:
Tứ giác ACHE có AE // HC và AE = HC.
Kết luận: ACHE là hình bình hành (tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành).
c) Chứng minh CK vuông góc với FI:
Xác định H là trung điểm của FC:
F thuộc tia AH và HA = HF => H là trung điểm AF.
H là trung điểm BC (cmt)
Mà C thuộc tia BH
Suy ra H là trung điểm FC
Chứng minh HI là đường trung bình của ΔFKC và suy ra HI // CK:
H là trung điểm FC (cmt)
I là trung điểm HK (gt)
=> HI là đường trung bình của ΔFKC => HI // CK (1)
Chứng minh IJ là đường trung bình của ΔFBC và ΔFHB
H là trung điểm FC (cmt)
IJ // BC (gt)
=> IJ là đường trung bình của ΔFBC
=> J là trung điểm FB
Mà I là trung điểm HK (gt)
=> IJ là đường trung bình của ΔFHB
=> IJ // FK (2)
Chứng minh K là trực tâm tam giác FKI:
Xét tam giác FHB có:HK ⊥ FB tại K
=> FK là đường cao
Từ (1) và (2) suy ra:HI // CK
Mà HI ⊥ FK (do HK ⊥ FB)
=> CK ⊥ FK
=> CK là đường cao
Mà FK và CK cắt nhau tại K
=> K là trực tâm tam giác FKI
Kết luận CK vuông góc FI:
K là trực tâm tam giác FKI (cmt).
=> IK ⊥ FI
Mà IK // CK (cùng ⊥ HK)
Kết luận: CK ⊥ FI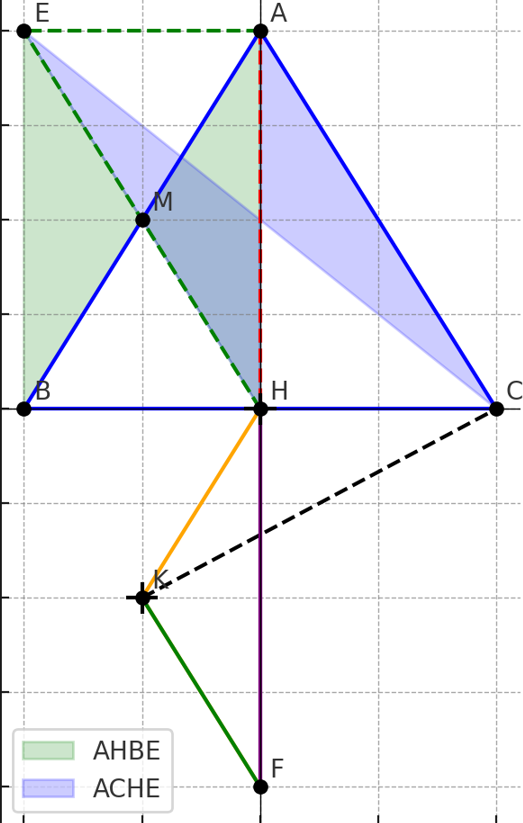
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
9908
Đã trả lời bởi chuyên gia
9908 -
 Đã trả lời bởi chuyên gia
7703
Đã trả lời bởi chuyên gia
7703


