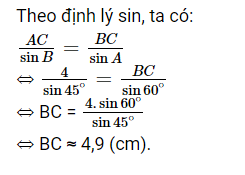Để tìm độ dài cạnh \( BC \) trong tam giác \( ABC \) với các thông tin đã cho: \( AC = 4 \, \text{cm} \), \( \angle A = 60^\circ \), và \( \angle B = 45^\circ \), chúng ta có thể sử dụng định lý sin.

Trước hết, chúng ta tính góc \( C \):
\[
\angle C = 180^\circ - \angle A - \angle B = 180^\circ - 60^\circ - 45^\circ = 75^\circ
\]

Sau đó, theo định lý sin:
\[
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
\]
Trong đó:
- \( a = BC \) (cạnh đối diện góc \( A \))
- \( b = AC = 4 \, \text{cm} \) (cạnh đối diện góc \( B \))
- \( c = AB \) (cạnh đối diện góc \( C \))

Chúng ta có:
\[
\frac{BC}{\sin A} = \frac{AC}{\sin B}
\]

Thay các giá trị vào:
\[
\frac{BC}{\sin 60^\circ} = \frac{4}{\sin 45^\circ}
\]

Biết rằng:
- \( \sin 60^\circ = \frac{\sqrt{3}}{2} \)
- \( \sin 45^\circ = \frac{\sqrt{2}}{2} \)

Thay vào phương trình:
\[
\frac{BC}{\frac{\sqrt{3}}{2}} = \frac{4}{\frac{\sqrt{2}}{2}}
\]

Giải phương trình:
\[
BC = \frac{4}{\frac{\sqrt{2}}{2}} \cdot \frac{\sqrt{3}}{2}
\]
\[
BC = 4 \cdot \frac{2}{\sqrt{2}} \cdot \frac{\sqrt{3}}{2}
\]
\[
BC = 4 \cdot \frac{\sqrt{3}}{\sqrt{2}}
\]
\[
BC = \frac{4\sqrt{3}}{\sqrt{2}} = 2\sqrt{6}
\]

Vậy độ dài của cạnh \( BC \) là:
\[
BC \approx 4.899 \, \text{cm} \quad \text{(tính gần đúng)}
\]

Do đó, giá trị của cạnh \( BC \) là \( 2\sqrt{6} \, \text{cm} \) hoặc khoảng \( 4.9 \, \text{cm} \).